Calcule a integral
Onde R é a região do primeiro quadrante limitada pela elipse . Use a mudança de variáveis e.
Passo 1
Bom, se pediram pra a gente fazer essas mudanças de variáveis, quem somos nós pra dizer que não, né?
Não vamos esquecer, poooor favor, o jacobiano.
Passo 2
Logo ficamos com
Daqui a gente muda mais pra coordenadas polares! Vê o ()?! É o sinal! (Por favor, mais uma vez, não esquece o Jacobiano. Já pensou deixar de ganhar os pontos da questão por conta dessa bobeira? Mas vamos lá que já está acabando)
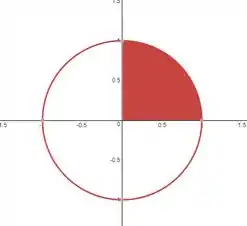
Lembra que a gente quer o primeiro quadrante, beleza? Então e .
Bora fazer uma substituição simples aqui, onde e correr pra o abraço.