Calcule
Onde é a região trapezoidal com vértices , , e .
Passo 1
Bem, dá pra ver que esse termo dentro do cosseno não tá muito agradavel... Mas vamos tentar então uma mudança de variável que se a gente conseguir fazer
Fica que aí é molezinha.
Só temos que ver se nosso domínio ajuda, então vamos ver como que fica isso.
Passo 2
Se marcarmos os pontos e fizermos um esboço do nosso domínio, a gente fica com:
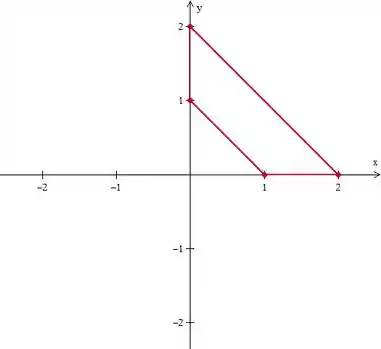
Ou seja temos as retas:
O que já ajuda, porque essas duas últimas aí vão fica, com a nossa transformação:
As outras duas também não é muito díficil de ver porque se jogarmos naquelas nossas equações lá em cima, vamos ficar com:
Para
Então .
A mesma coisa a gente faz para
Então .
Nosso domínio fica , .
Passo 3
Agora vamos calcular o jacobiano, mas como temos o e isolados, ao invés de e , vamos calcular primeiro o :
E vamos lembrar que:
Então pra integral, vai ficar:
E agora á só calcular!
Passo 4
É só integrar primeiro em :
E agora integramos em :
Já tá tudo resolvido, mas só ora ficar bonitinho, vamos lembrar que , então:
Seno de 1, que resposta é essa, ne??
Mas acontece, se eles querem ficar botando gabarito maluco assim, a gente não tem o que fazer, o que importa é que essa é a resposta!