Considere e a integral dada por
- Usando mudança de variáveis , encontre a região tal que e esboce e
- Determine a matriz jacobiana
- Calcule a integral dada usando a fórmula de mudança de variáveis para . Justifique.
Passo 1
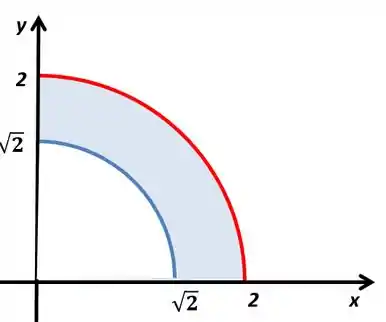
Vamos começar entendo como é a região . Consegue perceber que temos duas circunferências?
Essa tem raio e centro em
Essa tem raio e centro em
A região vai ser a região interna a circunferência maior e externa a circunferência menor, conseguimos ver isso pela desigualdade das equações. Além disso, vamos ter e , então estamos pegando a parte do quadrante. O seu gráfico vai ficar
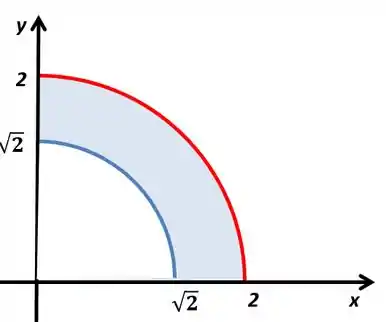
Passo 2
Vamos fazer agora a substituição
Vamos ter
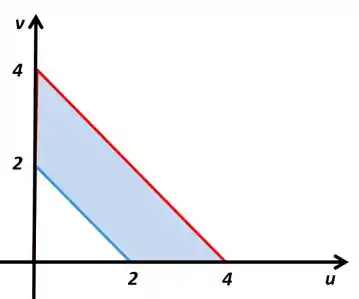
Vamos continuar tendo a limitação do primeiro quadrante, porque para e temos e , a diferença é que em vez de circunferências, vamos ter retas.
A região vai ser entre essas duas retas
O gráfico de vai ficar
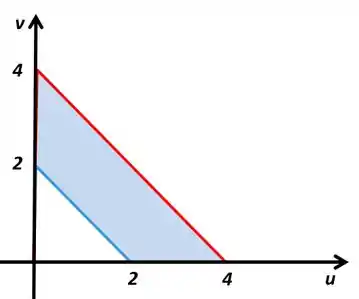
Passo 3
Temos
Passo 4
Vamos agora achar a integral que ele pediu. Para isso precisamos achar os intervalo que varia e , um vai ser limitado por números, e outro por funções. Vamos limitar por números. Conseguimos ver pelo gráfico que vai de à .
O problema é o valor de , olha como na verdade é
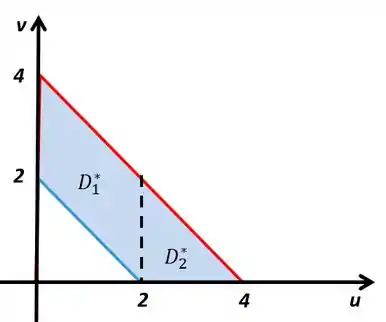
São duas partes, uma onde vai de uma reta, no caso , até a outra, . E a outra parte vai de até a reta .
Na primeira parte o valor de vai de à , e na segunda parte o valor de vai de à 4.
Vamos ter
E
Passo 5
A integral vai ficar
Resposta