Considere a integral
Onde .
- Usando a mudança de variáveis , esboce cuidadosamente a região tal que , justificando.
- Calcule a derivada .
- Calcule a integral dada usando a fórmula de mudança de variáveis.
- Cheque o resultado do item (c) calculando a integral nas variáveis .
Passo 1
Letra a)
A mudança que o problema pede nos dá que:
Assim passa a ser
E
Passa a ser
Substituindo em vemos que:
Assim, o outro intervalo que limita nossa região é
Foi? Temos e , graficamente:
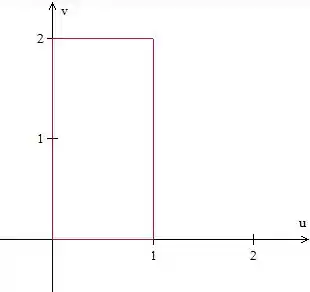
Passo 2
Letra b)
Nós temos:
Como
Passo 3
Letra c)
Agora vamos fazer essa mudança de variáveis na ntegral:
Agora é só calcular isso aí
Agora fazemos a substituição ,
Passo 4
Letra d)
Agora vamos calcular a integral sem fazer a mudança de variáveis:
Agora fazemos a substituição ,
Ainda bem que deu a mesma coisa né! Pronto, isso aí gente.
Resposta
- e