Considere a região limitada pela curva e pelos eixos coordenados. Determine
Dica: utilize a transformação de coordenadas , .
Passo 1
Antes de tudo, vamos fazer um esboço da região para entender melhor o que está sendo pedido.
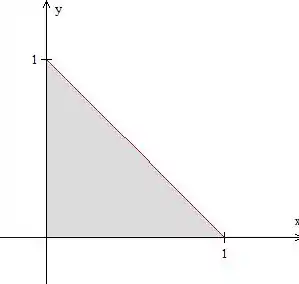
A região é essa marcada em cinza.
Passo 2
Ok, e agora? No plano , podemos escrever essa região como tipo I, está entre as retas e e vai de a , portanto:
Fazendo a mudança sugerida
Temos
O que nos dá
Bom, no plano podemos então descrever a região como
Passo 3
Bom, mas como tudo na vida tem um preço, não poderia ser tão simples assim né.
Temos que calcular o Jacobiano dessa transformação, lembra?
Temos:
Isso nos dá
Passo 4
Beleza, agora vamos montar a integral:
Passo 5
Agora é só resolver isso aí
Agora vamos fazer a mudança:
Levando para a integral
Substituindo
Temos