Seja a região delimitada pelo quadrilátero com vértices , , e .
a) Esboce a região no plano .
b) Considere a transfomação e . Esboce a imagem da região através da tranformação no plano .
c) Calcule
Passo 1
a)
Bem, essa é aquela questão pra não tirar zero na prova, né? Vamos só marcar os pontos e ligá-los, coisa básica:
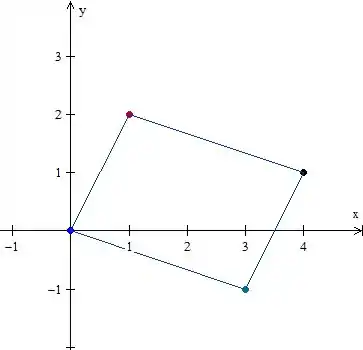
Não tem com errar! haha
Passo 2
b)
Agora já começa a complicar um pouco, temos que fazer a substituição e tal, ele pede que:
Mas vamos começar tentando entender como são aquelas retas do quadrilátero nas coordenadas cartesianas. A nossa região era limitada por quatro retas, de equações:
Que são resultados muito convenientes, porque com as transformações, vamos ter:
Passo 3
Agora é só traçar essas retas no plano :
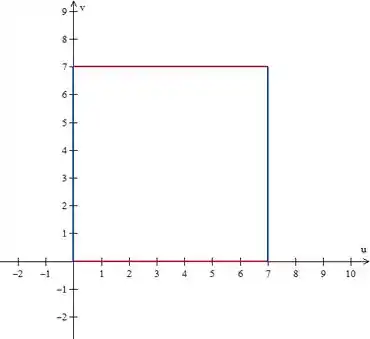
Passo 4
c)
O cara ficou esse tempo todo enrolando, pedindo desenho, mas agora vem a parte séria, vamos ver essa integral aí!
Mas isso não vai ficar muito difícil justamente porque já temos nossa transformação:
Agora vamos calcular o jacobiano. Mas como temos e isolados, ao invés de e , vamos começar por :
Então, vamos ter o determinante:
Mas como:
Agora é só calcular a integral!
Passo 5
Vamos substituir tudo na integral, inclusive os limites, que vimos pelo desenho que são e vamos ter:
Que resultado esquisito, hein? Mas é isso mesmo!
Resposta
a)
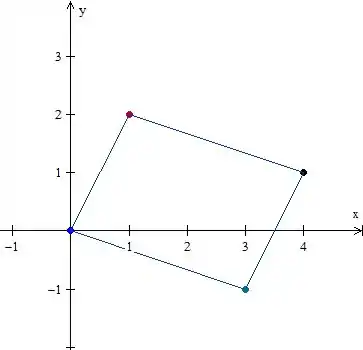
b)
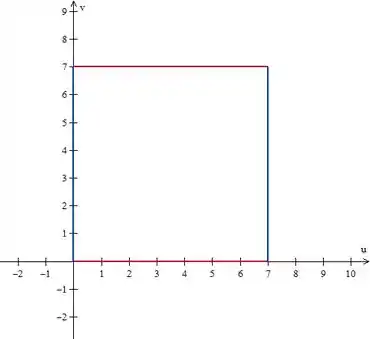
c)