Era uma vez um plano encantado. Neste plano, os habitantes eram os pontos. Um dia, um ponto cientista decidiu medir o quanto cada habitante era legal e criou uma função que media isso. A função era dada por
.
Quanto maior o valor de , mais legal o ponto era.
Determine os pontos mais legais e mais chatos da região
.
Passo 1
Eaew, belezinha?
A função mede o quanto legal uma pessoa é, ou seja, se queremos saber quem é a pessoa mais legal, temos que procurar o máximo da função
.
na alternativa anterior nós usamos o método de multiplicadores de lagrange, construído tal que
em que e são as derivadas parciais em relação a e . E, a função era uma restrição obtida através da curva
E, obtemos os pontos de máximo como
e
e, os pontos de mínimo como
Mas, qual a diferença para esta alternativa? Note que temos ao invés da curva, a região
ou seja, ao invés de estarmos trabalhando puramente na borda da circunferência, iremos estar analisando toda a região interna a ela! Saca só como isso vai mudar o nosso problema!
Passo 2
Vamos dar uma olhada na região, temos que
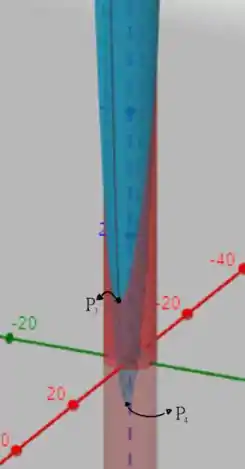
O cilindro vermelho indica a nossa região, note que e continuam sendo os pontos de máximo! Mas, uma vez que não estamos considerando mais apenas as bordas, deixa de ser o ponto de mínimo! O novo mínimo será dado por indicado na figura da esquerda! Vamos tentar achá-lo!
Passo 3
Agora, para achar esse mínimo, vamos precisar aplicar outros métodos que não o de multiplicadores de lagrange! E, para começar, precisaremos verificar os pontos críticos de nossa função, ou seja, onde as derivadas parciais são iguais a zero, nós calculamos na alternativa anterior que
e
obtemos então o ponto que tem coordenadas e . Mas, como garantimos que isso é mínimo? Pelo gráfico é bastante óbvio, mas vamos fazer isso matematicamente! Precisamos analisar a matriz Hessiana dada por
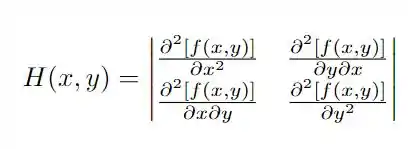
teremos as três situações, se no ponto crítico , termos , então o ponto é um máximo ou mínimo, se temos um ponto de sela, e se , não podemos determinar! Quando chegar a hora eu apresento como diferenciar entre o máximo e mínimo! Vamos calcular agora as nossas segundas derivadas, já que iremos precisar! Saca só!
Passo 4
Calculando as derivadas em relação a , tomamos como constante, isso resulta em
e
em que usei a regra do tombo
e que a derivada de constante é igual a . Agora, se derivarmos em relação a , temos que
e
Substituindo em nossa matriz, e calculando o determinante, obtemos que
Como , temos que esse é um ponto de máximo, ou mínimo! Como sabemos qual? É apenas analisar a condição
Mínimo: e Máximo:
Sendo assim, temos um ponto de mínimo! Ou seja, o nosso ponto é tal que , substituindo as coordenadas em nossa função, obtemos que
Resumindo, temos que
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Pontos mais legais são e e o mais chato