A interseção entre plano e cone é uma elipse .
a) Esboce o cone, o plano e a elipse.
b) Determine os pontos na elipse que estejam mais próximo e mais distante da origem.
Dica: use a fórmula da distância no espaço com três dimensões. Para facilitar as contas, você pode elevar esta fórmula ao quadrado (explique o porquê).
Passo 1
a) Vamos começar pelo cone! Como os termos ao quadrado são só as variáveis sozinhas , a gente pode dizer que o centro do nosso cone é a origem, o ponto .
E como os termos ao quadrado e estão mutltiplicado por , nosso cone vai ser um pouco mais fechado que o cone , por exemplo. Ele fica assim
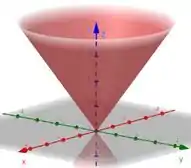
Agora para desenhar o plano , vamos achar onde ele corta os eixos coordenados. Aí a gente desenha um plano que passa por esses pontos.
O ponto que passa pelo eixo , tem . Substituindo na equação
Fazendo algo parecido para os outros eixos
Aí a gente precisa esboçar um plano que passa pelos pontos e Ele fica assim:
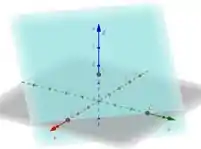
E para desenhar a elipse, a gente faz essas duas superfícies no mesmo espaço e marca a interseção entre elas:
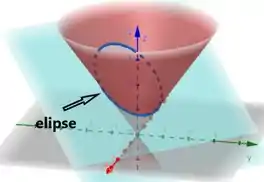
Ali a gente achar uma elipse no espaço 3D, como o enunciado diz! Arrasamos nessa!
Passo 2
b) A fórmula da distância entre a origem e um ponto no espaço tridimensional é
A gente quer a máxima e a mínima distância. Então queremos maximizar e minimizar . Mas ele disse que para faciitar as contas, a gente pode usar . E por que? Essa é a :
Uma função com raiz quadrada é muito mais dificil de derivar. E a gente precisa fazer calcular derivadas para achar o máximo e mínimo de uma função.
E a gente pode fazer essa mudança porque a função e a função tem os mesmos pontos de máximo e de mínimo. Então podemos usar qualquer uma delas, beleza?
Então vamos maximizar e minimizar a função
Passo 3
Cara, mas quem são esses valores de para gente? São os pontos que estão dentro da elipse, né? E quem é a elipse? A interseção entre o plano e cone .
Os pontos da elipse pertencem ao mesmo tempo a essas duas superfícies. Ou seja, nossos precisam satisfazer essas duas equações.
Percebe o que a gente tem aqui? Temos que maximizar uma função , mas estão restringidos a duas equações. Isso quer dizer que temos que usar os multiplicadores de Lagrange com duas restrições!
Nossas restrições são
A gente faz essas mudanças nas equações que são nossas restrições: joga todas as variáveis para um lado e chama o lado das variáveis de uma função nova:
E agora é montar a fórmulinha
Por ela a gente acha os nossos pontos. Vem comigo!
Passo 4
Vamos calcular os gradientes de cada função
Aí a nossa fórmulinha fica
Daí tiramos as equações
Agora a gente monta um sisteminha com essas equações e as equações que são nossas restrições. Fica assim:
Partiu resolver esse cara na coragem! Segura na minha mão e vem!
Passo 5
Vamos dividir os dois lados da terceira equação por , só para ficar fofo:
As duas primeiras equações têm um termo em comum, vamos isolar esse termo nelas
Igualando essas duas coisinhas
Agora calma: dá para cortar esse termo dos dois lados né? Mas antes, a gente precisa avaliar a situação onde esse termo zera, porque isso também satisfaria nossa equação. Fica assim
Aí sim, a gente pode voltar para aquela equação e cortar esse termo
Ficamos então com duas situações para avaliar: ou .
Passo 6
Vamos começar avaliando o caso em que
Substituindo na primeira equação
Substituindo e na terceira
E substituindo na quarta equação
O único ponto que satisfaz essa equação é , porque temos uma soma de termos positivos dando zero. Então a gente achou o ponto . Mas repara que se a gente o substituir na equação do plano
Ele não satisfaz a equação do plano. Então esse ponto não serve para a gente, tá?
Passo 7
Mas calma, ainda tem o caso . Tenha esperança!
Substituindo na última equação
Aparece esse porque tiramos a raiz ali. Aí agora se abriram dois caminhos:
- Substituindo e na equação do plano
Daí a gente tira que
Temos então o ponto .
- Substituindo e na equação do plano
Daí a gente tira que
Temos então o ponto .
Passo 8
Agora a gente substitui nossos candidatos na função que queremos maximizar e minimizar para ver quem vai ser o ponto de distância máxima e o ponto de distância mínima.
Para o ponto :
Para o ponto :
Como , o nosso ponto de máximo é , e esse é o ponto da elipse mais distante da origem.
E o nosso ponto de mínimo é , e ele vai ser o ponto da nossa elipse que tem a menor distância em relação à origem.
Resposta
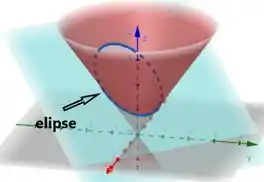
Ponto mais próximo da origem:
Ponto mais distante da origem: