Considere as bases. , e , bases de ,respectivamente . Se é a transformação linear tal que:
é:
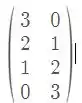
Então
é:
Passo 1
Fala pessoal, tudo beleza com vocês? Vamos para mais uma questão de Algelin, dessa vez estaremos trabalhando com matriz de mudança de base. Muito bacana, né? Nosso objetivo nessa questão é descobrir quem é a transformação linear que leva os vetores de para um polinômio formado com os elementos da base de . Vamos nessa!!

Passo 2
Como comentei no passo 1, essa é uma questão que envolve mudança de base. Existe um teorema que diz como podemos relacionar uma transformação linear entre dois espaços de dimensão finita quaisquer. Lembram dele? Vamos revisar!!!!
O Teorema diz o seguinte,
Ou seja nossa transformação fica:
Já temos , mas quem é ?

Passo 3
No passo anterior revisamos o teorema que diz como construir a matriz que representa a transformação linear entre dois espaços de dimensão finita. Mas observamos que era necessário saber , mas quem é esse vetor?
Essa notação indica que estamos transformando o vetor representado na base canônica para sua representação na base . Como fazemos isso?
Pode parecer difícil, mas não é. Só precisamos escrever o vetor como combinação linear dos elementos da base de . Vamos fazer, que ficará mais claro. Nosso objetivo então é encontrar
tais que:
Resolvendo obtemos
Então nosso vetor
será:

Passo 4
Pronto, agora podemos calcular
Na forma matricial fica:
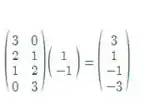
Portanto,
E para finalizarmos a questão, precisamos dessa transformação linear gerada por esse vetor. Como estamos na base temos:
(calculando o produto interno)
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊