Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Transformação Linear

Ver Teoria
Exercício 681234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666769707172

Enunciado

USP; Sem campus; Algebra Linear 2; P2; 2022; Questão 1

Seja T   :   R 2   →   R 4 a transformação linear tal que

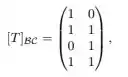
em que B denota a base canônica de R 2 e C denota a base canônica de R 4 . Se a ,   b   ∈   R são tais que ( a ,   b ,   1 ,   3 ) pertence à imagem de T , então a + b é igual a:

(a) 5

(b) 4

(c) 0

(d) 7

(e) − 2

Passo 1

Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Dessa vez vamos trabalhar com uma transformação linear. Temos que

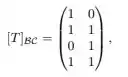
é a transformação de interesse. Mas vish, não temos T temos apenas a matriz de transformação de base. E agora? Agradece, pois a transformação T está operando sobre a base canônica, logo a nossa T B C é a nossa matriz T . Bacana, ne?

Nosso objetivo é calcular a + b , sabendo que ( a ,   b ,   1 ,   3 ) pertence à imagem de T

Passo 2

Como ( a ,   b ,   1 ,   3 ) pertence a imagem de T , temos que :

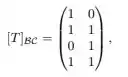
Temos:

( a ,   b ,   1 ,   3 ) = t ( 1,1 , 0,1 ) + s ( 0,1 , 1,1 )

Então

( a ,   b ,   1 ,   3 ) = ( t , t + s , s , s + t )

Analisando, podemos dizer logo de cara que

s = 1

t = a

Logo

s + t = 1 + a

s + t = b

s + t = 3

Juntando a primeira e última equação, temos que

a = 2

e

b = 3

Portanto, a + b = 5

Valor presente na alternativa a )

Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

a )

Exercícios de Livros Relacionados

Uma transformação linear T:R ²→R ² ² ² de posto 2 transforma toda reta numa reta. Prove isto.
De um exemplo de uma transformação linear T sobrejetiva e não injetiva. Prove que é sobrejetiva e não injetiva.
Prove que uma transformação linear é injetiva se, e somente se, seu núcleo se reduz ao único elemento 0 ∈ R 3
Prove que, para toda transformação linear M : R 3 →R 3 , a transformação M * M é auto adjunta e que o núcleo de M * M coincide com o núcleo de M . Em particular, se M é invertível, o mesmo ocorre M *
Chama-se núcleo da transformação linear M : R 3 → R 3 ao conjunto N M = { v ∈ R 3 ; M v = 0 } . Determine os núcleos das transformações lineares dos exemplos 47.1 ,47.2 ,47.3e47.4 . prove que se u , v