Seja a transformação linear definida por
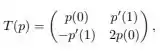
para todo . Temos que
é igual a:
(a)
(b)
(c)
(d)
(e)
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Dessa vez vamos trabalhar com núcleo e imagem de uma transformação. Bem, nossa transformação de interesse é dada pela matriz
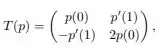
onde
E queremos calcular

Passo 2
Vamos começar calculando a imagem do núcleo da nossa transformação.
Seja
Então,
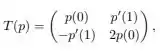
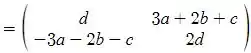
Para pertencer ao núcleo, precisamos que . Logo, usando a matriz acima, obtemos as seguintes condições
Note que a segunda equação tem duas variáveis livres. Logo a dimensão do núcleo será , e será dada pelos polinômios tais que
Já temos a imagem do núcleo de , vamos obter a dimensão da imagem.

Passo 3
Vamos descobrir a dimensão da imagem de . Para isso, podemos usar o teorema do núcleo e da imagem. Lembram dele? Ele diz que se transformação linear, então
No nosso caso, que tem dimensão , pois uma base para esses polinômios é
Logo, temos que
Ou seja, temos que
Valor presente na alternativa

Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta