Considere a matriz
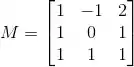
e a transformação linear cuja matriz na base canônica é M.
(b) Determine as coordenadas na base canônica do vetor v que verifica
Passo 1
(b) Se então:
Vamos dizer que
Então:
Escrevendo na forma de matriz aumentada e escalonando:


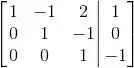
Da terceira linha:
Substituindo na segunda linha:
Substituindo na primeira:
Portanto, o vetor é:
Resposta
(b)