À questão “Dado fixo, a transformação dada por é linear?”, Andrezinho respondeu da seguinte maneira:
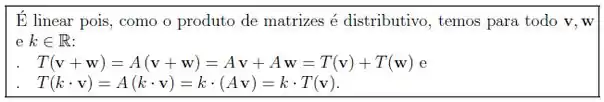
a) Embora seja realmente uma transformação linear, a justificativa do Andrezinho não está correta. Qual foi o erro que ele cometeu?
b) Mostre que é linear.
Passo 1
Andrezinho errou a expressão da e também quem são os elementos do seu domínio. Assim, ele fez variar o vetor coluna enquanto seu domínio é na verdade , ou seja quem deveria variar deveria ser uma matriz e não um vetor coluna!
Assim, ele fixou matriz , e tomou como suas variáveis do problema, provando para uma dada por e não uma dada por .
OBS: Talvez você tenha confundido que , também. Pois o jeito que ficou escrito, ficou meio confuso. Mas não tem problema pensar que seriam números reais e não vetores colunas. Uma justificativa com esse argumento também é válida.
Passo 2
Antes de começar, NÃO É NECESSÁRIO EXPANDIR A MATRIZ COMO UMA !! BASTA USAR AS PROPRIEDADES DAS MATRIZES!
Assim para provar que é linear basta fazermos:
Vamos provar essa primeiro:
Desenvolvendo o lado temos que:
E assim vemos que !
Passo 3
Agora vamos provar que
Assim, vamos desenvolver o lado :
E assim podemos ver que os lados e são iguais, E, portanto provamos as condições para nossa ser linear!
Resposta
Ei, a resposta está no passo a passo :)