Uma partícula de massa move-se inicialmente com velocidade de módulo ao longo de uma trajetória retilínea que forma um ângulo de com o eixo , como mostra a figura. Ela colide com uma segunda partícula que tem duas vezes sua massa, isto é , que está movendo-se ao longo da direção e sentido positivo com velocidade de módulo três vezes maior que , ou seja: . Depois da colisão, a primeira partícula move-se ao longo da direção e sentido negativo, enquanto que a segunda partícula continua a mover-se ao longo do eixo e sentido positivo, com uma velocidade escalar reduzida. Considere que não atuam forças externas sobre as partículas. Se na solução de algum item abaixo for usada alguma lei de conservação, justifique-a.
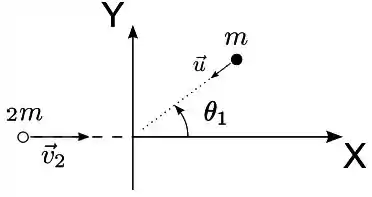
- Determine o vetor momento linear total inicial para este sistema de duas partículas;
- Calcule os módulos das velocidades de ambas as partículas depois da colisão em função dos dados do problema;
- Determine o vetor velocidade do centro de massa do sistema antes e depois da colisão.
Dados: ; .
Passo 1
a)
Para acharmos o momento linear total inicial devemos achar o momento linear de cada partícula, para a partícula
Então
Passo 2
Para a partícula temos que decompor as componentes da velocidade, usando a regra do “COlado/SEparado”
Ambos são negativos porque o corpo vai para esquerda e para baixo.
Escrevendo isso vetorialmente
O momento linear fica
Passo 3
O momento linear inicial do sistema fica
Passo 4
b)
Como não temos forças externas atuando o momento linear é conservado
A velocidade da partícula vai ser
E seu momento linear
Enquanto a velocidade da primeira partícula vai ser
E seu momento linear
Dando o seguinte momento linear do sistema
Isso segundo os dados do enunciado. Lembrando que ai temos os módulos das velocidades
Passo 5
Igualando ao momento linear inicial
Vamos encontrar
E
Essas velocidades tem o mesmo sinal do enunciado. : )
Passo 6
c)
A velocidade do centro de massa pode ser calculada pelo momento de inércia do sistema como já vimos nos exercícios de fixação
Como momento linear se conserva após a colisão,
a gente pode concluir que a velocidade do centro de massa é a mesma antes e depois da colisão.
Resposta
- , antes e após a colisão.