Em um dos últimos jogos olímpicos de inverno, a final de Curling foi disputada entre Canadá e Rússia. O jogo consiste em posicionar pedras dentro de um alvo. Em uma de suas jogadas a equipe canadense realizou uma proeza típica de uma equipe vencedora. A figura abaixo representa a pista de gelo vista de cima. As duas pedras e da equipe russa estão em repouso e foram posicionadas durante o jogo. Uma terceira pedra a ser lançada pela equipe canadense está também ilustrada. A pedra lançada com velocidade , consegue acertar a pedra russa em uma colisão elástica bidimensional expelindo para fora do alvo com uma velocidade de módulo , sua trajetória faz um ângulo com a horizontal. Na sequencia a pedra faz uma segunda colisão elástica unidimensional com a pedra expelindo-a para fora do alvo. Considere todo atrito entre as pedras e o solo eliminado pelos outros membros das equipes com suas vassouras. Considere as massas de todas as pedras .
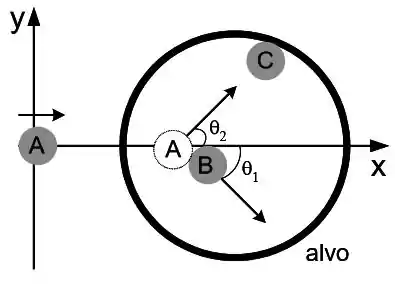
a) Determine a velocidade do centro de massa antes da primeira colisão.
b) Encontre o ângulo e a velocidade da pedra ao final da primeira colisão com a pedra .
c) Calcule a força média exercida pela pedra sobre a pedra durante a colisão que durou .
d) Considere agora a colisão entre as pedras e . Encontre e ao final da segunda colisão.
Passo 1
(a)
Basta utilizar a fórmula:
Substituindo os dados:
Passo 2
(b)
Fazendo a conservação do momento linear, temos:
No eixo :
Substituindo os dados:
No eixo :
Substituindo os dados:
Fazendo /:
Logo o vetor será:
Passo 3
(c)
Utilizando a fórmula da força média em :
A força média em possui a mesma intensidade mas com o sentido invertido, logo:
Passo 4
(d)
Como a colisão é elástica e unidimensional, eles irão apenas trocar as velocidades um com o outro:
Resposta
(a)
(b)
(c)
(d)