No referencial da Terra o está se aproximando com velocidade do , que está inicialmente em repouso. Os carros estão em um trilho de ar e o tem cinco vezes a inércia do . Eles colidem elasticamente. Calcule as velocidades antes e depois da colisão:
No referencial da Terra.
No referencial de momento zero.
Faça um gráfico do momento linear dos carros em função do tempo para o referencial de momento zero. Considere , e o tempo após a colisão. Coloque no gráfico os resultados para as velocidades obtidos no item precedente.
Passo 1
Vem comigo que a gente resolve essa juntos!
Nesse problema como temos uma colisão elástica, vamos ter conservação de energia e conservação de momento.
Vamos chamar a massa do de , logo a do vai ser .
Temos o seguinte para a conservação do momento:
Para a conservação da energia temos:
Dividindo o que encontramos na conservação da energia por o que encontramos na conservação de momento, temos:
E usando essa relação nas equações da conservação do momento e da energia que encontramos, temos o seguinte:
A partir dessas equações podemos encontrar tudo o que o enunciado pede, vamos chamar de referente ao e de referente ao .
Um conceito que aparece no enunciado é o de referencial de momento zero, nesse referencial o momento do sistema deve ser zero, que acaba sendo o referencial do centro de massa do sistema.
Então ara acharmos as velocidades dos carros nesse referencial, temos que saber a velocidade do centro de massa, dada por:
Tendo essa velocidade a gente consegue achar a velocidade dos carros nesse novo referencial.
Passo 2
Vamos começar com o item .
As velocidades antes da colisão já foram dadas, a do e do .
Para saber as velocidades depois da colisão vamos usar as equações que chegamos no passo para e , só temos que tomar cuidado com os índices.
Para o :
Usando que , e , temos:
Logo temos que:
Para o :
Substituindo com o que sabemos, temos:
Logo temos que:
Passo 3
Agora vamos para o item .
No referencial de momento zero, tanto o momento antes da colisão quanto o depois tem que ser zero e esse referencial que faz com o momento seja zero se move com a velocidade do centro de massa.
Vamos calcular essa velocidade então, temos:
Logo temos que:
Esse referencial se move na mesma direção que o , então a velocidade dele nesse referencial vai ser dada por:
E esse referencial se move contra o , assim a velocidade desse carro nesse referencial é dada por:
Esse sinal de menos é vem do fato que o está se movendo no sentido contrário.
Passo 4
Agora vamos ver para depois da colisão.
Depois da colisão o se move no mesmo sentido que o referencial do centro de massa, já que a velocidade que encontramos pra ele no referencial da Terra é positivo, assim:
O também se move no mesmo sentido do referencial do centro de massa, pelo mesmo motivo que o , assim:
Passo 5
Agora para o item temos que montar o gráfico do momento de cada carro no referencial de momento zero, antes e depois da colisão.
Primeiro temos que saber o valor desses momentos. Para o , temos:
Para o , temos:
Como não temos o valor da massa e de vamos montar um gráfico de . Então o gráfico fica da seguinte maneira:
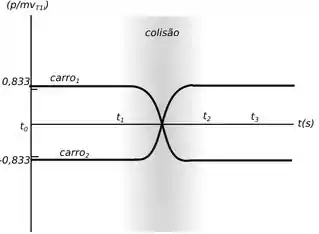
Resposta
:
:
:
: