Exercícios de Derivada da Função Inversa - Lista de Exercícios Resolvida
Questão 3
Considere a função inversa de . Sejam , . Determine:
Determine .
Determine .
Ver solução completaQuestão 4
Sejam , e funções reais de classe , com uma função inversível e
Calcule em termos de , , , e . Justifique sua resposta.
Calcule sabendo que , , , , e . Justifique sua resposta.
Ver solução completaQuestão 5
Seja para
A função é inversível?
Determine uma expressão pra a função , a inversa de
Calcule a derivada de em
Ver solução completaQuestão 6
Considere a função
Onde é uma constante.
Mostre que restrita a possui uma inversa
Determine
Determine
Determine um valor de tal que seja inversível em
Ver solução completaQuestão 7
Seja
a) Calcule
b) Determine , a derivada da função
c) A função é inversível? Justifique.
d) Determine a expressão para , a inversa da função
e) Esboce o gráfico de , assinalando os pontos onde o gráfico intercepta os eixos.
Ver solução completaQuestão 8
Considere a função inversa de . Sejam , E . Determine:
Determine .
Determine .
Determine .
Sugestão: derive duas vezes.
Ver solução completaQuestão 15
Questão 2:
Seja .
- Considere como domínio de o maior possível para que seja inversível e para que o gráfico de (a função inversa de ) passe pelo ponto . Nestas condições, determine o domínio de , o domínio de , e uma expressão para .
- Determine a equação da reta tangente ao gráfico de em .
Questão 16
Considere a função tangente:
Determine o maior intervalo contendo tal que a função tangente restrita a este intervalo seja inversível;
Seja a inversa da função mencionada no item , determine uma expressão para em função de ;
Calcule .
Ver solução completaQuestão 17
Seja :
Calcule a derivada de ;
A função possui inversa?
Seja , determine o valor de ;
Calcule a derivada da inversa de em ;
Ver solução completaQuestão 18
Enuncie a regra da derivada da função inversa. Use este resultado para calcular a derivada da
função
Ver solução completaQuestão 19
Seja para
- A funçã0 é inversível?
- Determine uma expressão pra a função , a inversa de
- Calcule a derivada de em
Questão 21
Seja
a) Determine , a derivada da função
b) Determine a derivada da inversa de em
Ver solução completaQuestão 23
Seja para
Determine uma expressão para a inversa de h neste intervalo
Esboce o gráfico de e da sua inversa no mesmo plano cartesiano
Ver solução completaQuestão 26
Seja:
Calcule a derivada de .
Determine um intervalo , o maior possível, tal que e que seja invertível.
Ver solução completaQuestão 31
Considere a função .
(a) Qual o maior conjunto onde a função inversa existe? Justifique.
Ver solução completaQuestão 35
Seja . Mostre que é invertível para todo e calcule a derivada da função inversa em .
Ver solução completaQuestão 36
6. Considere a função invertível representada no gráfico abaixo. Determine dentre os gráficos à direita qual melhor representa a função inversa .
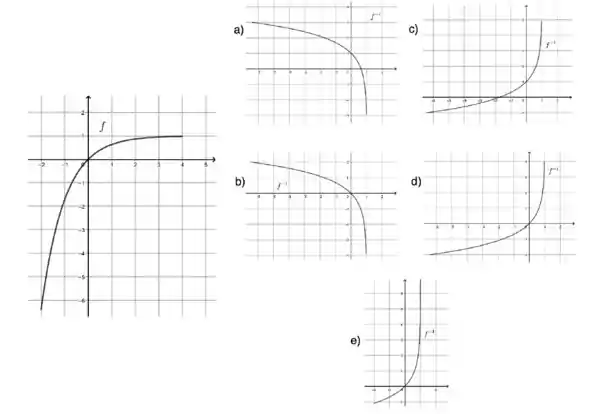
Questão 37
7. Considere a função definida em .
a) Determine a imagem de .
b) Determine
c) Determine a expressão da função inversa
Ver solução completaQuestão 39
Considere a função .
Determine .
Determine o maior intervalo contendo tal que seja invertível.
A reta tangente ao gráfico desta inversa de no ponto .
Ver solução completa