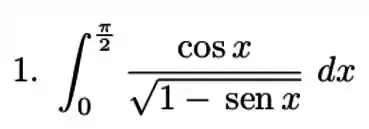
Passo 1
Temos uma integral imprópria já que ela não é continua, .
Para saber se a integral converge ou diverge precisamos aplicar o limite da integral e ver se dá um número finito. Se sim, então a integral é convergente. Se ao calcular o limite obtivermos um valor tipo , a integral é divergente.
Passo 2
Quando temos uma integral imprópria desse tipo, precisamos fazer
Passo 3
Agora vamos resolver a integral normalmente. Para isso vamos utilizar a substituição
Desfazendo a substituição
Aplicando os limites de integração
Passo 4
Aplicando o limite
O limite resultou em um número finito, logo a integral converge.
Resposta
Exercícios de Livros Relacionados
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ 0 1 1 1 - x 2d x
Investigar as integrais impróprias.
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ 0 1 3 x 5d x
Explique por que cada uma das seguintes integrais é imprópria. ∫ 1 ∞ x 4 e - x 4 d x ∫ 1 π 2 sec x d x ∫ 0 2 x x 2 - 5 x + 6 d x ∫ - ∞ 0 1 x 2 + 5 d x
Calculeb)int_(- 1)^3 f (x) d x ondef (x) = {[[1 s e - 1 = x0],[x^2 s e 0x2],[0 s e 2 = x = 3]])