UnB; Introdução à Álgebra Linear; 1ª Lista de Exercícios – Turma E; Exercício 28d
28) Encontre a inversa das matrizes:
Passo 1
Opa pessoas lindas desse mundãooo do Responde Aí!! Leu esse enunciado e ficou um pouco confuso?
Calma, vamos resolver juntos com muito amor e carinho hehehehehe. Vamos que vamos!!
O enunciado nos deu uma matriz e pediu pra gente encontrar a inversa dessa matriz. Mas como é que a gente faz isso? O que é uma matriz inversa?
Uma matriz inversa é uma matriz quadrada, ou seja, que possui o mesmo número de linhas e colunas. Tá, mas o que eu devo fazer pra encontrar a matriz inversa?
Como aqui temos uma matriz , vamos utilizar o método da eliminação de Gauss. Mas nossa, o que é isso?
O método da eliminação de Gauss permite acharmos a matriz inversa de maneira mais fácil e menos propensa a erros! Conforme formos resolvendo-a, você vai entender bem melhor o porquê disso!
Além disso, vamos dizer que a matriz é a inversa de e é representada por !
E vale lembrar de mais uma coisinha também: só teremos uma matriz inversa quando o determinante for diferente de zero, ok?
Falando assim parece meio estranho, né? Mas bora lá resolver isso que você vai ver como é tranquilinho!
Passo 2
Vamos começar então, checando se o determinante da matriz é diferente de zero, para que possamos ter uma matriz inversa!
Como temos uma matriz , para encontrar seu determinante, vamos primeiro duplicar suas duas primeiras colunas, e em seguida fazer a soma da multiplicação dos elementos da diagonal principal, subtraído da soma da multiplicação dos elementos da diagonal secundária!
Vamos chamar aqui de: a soma dos que foram, menos a soma dos que voltaram hahaha! Bora lá então:
Uhul! O determinante deu diferente de ! Bora lá calcular a matriz inversa então!
Passo 3
Agora vamos aplicar o método da eliminação Gaussiana para encontrarmos a inversa!
Para começar, vamos aumentar a nossa matriz original , ao adicionar uma matriz identidade também ao seu lado!
Lembre-se que a matriz identidade é definida quando os elementos da diagonal principal são todos iguais a e o restante dos elementos é !
Então teremos algo assim:
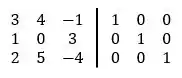
Tá, mas e agora o que eu faço com isso?
Vamos efetuar operações elementares, de modo que o lado esquerdo passe a ser a matriz identidade, e o lado direito torne-se a nossa inversa!! Ou seja, teremos o seguinte:
Vamos lá realizar essas operações então!
Passo 4
Relembrando nossa estrutura que sofrerá as operações elementares:
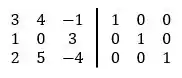
Para realizar as operações, chamaremos as linhas e respectivamente de e , e vamos ter um único objetivo em mente, que não é o de encontrar a matriz inversa, mas sim, fazermos surgir a matriz identidade do lado esquerdo!!
Esse pensamento vai ser a chave pra gente descobrir que operações devemos fazer!!!
Vamos começar multiplicando cada elemento de por :
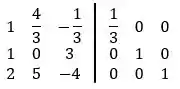
Agora faremos: :
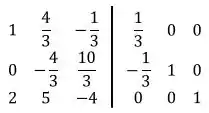
Seguindo, faremos: :
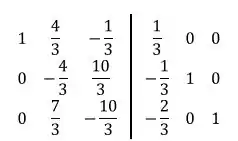
Multiplicaremos então por :
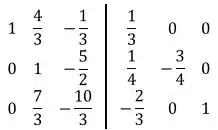
Faremos agora a operação de linha: :
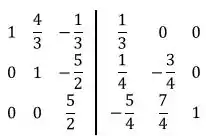
Multiplicaremos cada elemento de por :
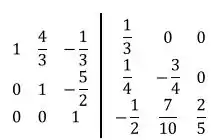
Faremos a operação de linha: :
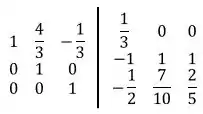
Faremos a operação de linha: :
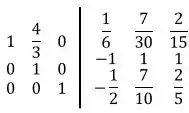
E, por fim, vamos fazer a operação: :
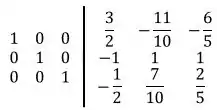
Olha só que legal! Todas as operações que realizamos foi com o objetivo de fazer surgir a matriz identidade do lado esquerdo, e foi exatamente isso que aconteceu!
Agora sabemos que a matriz presente do lado direito é a nossa matriz inversa !
Uhul! Nem foi tão difícil assim, vai!
Bora lá resolver mais uma questãozinha, então?