Exercícios de Distribuição Poisson - Lista de Exercícios Resolvida
Questão 1
Você vai fazer uma análise estatística com dados de carros que passam pelas catracas do estacionamento da PUC – Rio. Foram coletados a quantidade, marcas e placas dos veículos que entraram no estacionamento em 1 semana (segunda a sábado; 6 dias).
Considerando somente o último algarismo das placas dos veículos da amostra (0 a 9), responda: (identifique qual é o modelo probabilístico em cada caso).
a) Pelos dados, durante toda a semana (segunda a sábado), passaram pelas catracas 5 carros da marca BMW no estacionamento; ou seja, um evento realmente “raro”. Qual a probabilidade de entrar mais que 2 carros da marca BMW em um dia qualquer da semana?
Ver solução completaQuestão 2
- Defina um experimento que caracterize uma variável aleatória Poisson. Dê um exemplo real.
Ver solução completaQuestão 3
Suponha que a probabilidade de que um item produzido por uma máquina seja defeituoso é de 0,2. Se dez itens produzidos por essa máquina são selecionados ao acaso, qual a probabilidade de que não mais do que um defeituoso seja encontrado? Use a binomial e a distribuição de Poisson e compare os resultados.
Ver solução completaQuestão 4
Num certo tipo de fabricação de fita magnética, ocorrem cortes a uma taxa de um por 2.000 pés. Qual a probabilidade de que um rolo com 2.000 pés de fita magnética tenha:
a) Nenhum corte?
b) No máximo dois cortes?
c) Pelo menos dois cortes?
Ver solução completaQuestão 5
Em uma seção de uma auto-estrada, o número de buracos, que é bastante significante para requerer reparo, é suposto seguir uma distribuição de Poisson com média de dois buracos por quilômetro.
- Qual é a probabilidade de que não haja buracos que requeiram reparo em 5 de auto-estrada?
- Qual é a probabilidade de que no mínimo um buraco requeira reparo em 0,5 de auto-estrada?
- Se o número de buracos estiver relacionado à carga do veículo na auto-estrada e algumas seções dessa auto-estrada estiverem sujeitas a uma carga pesada de veículos, enquanto outras seções estiverem sujeitas a uma carga leve de veículos, como você se sente a respeito da suposição de distribuição de Poisson para o número de buracos que requeiram reparo?
Questão 6
O número de petroleiros que chegam a uma refinaria em cada dia ocorre segundo uma distribuição de Poisson, com . As atuais instalações podem atender, no máximo, a três petroleiros por dia. Se mais de três aportarem num dia, o excesso é enviado a outro porto.
a) Em um dia, qual a probabilidade de se enviar petroleiros para outro porto?
b) De quanto deverão ser aumentadas as instalações para permitir atender a todos os navios que chegarem pelo menos em 95% dos dias?
c) Qual o número médio de petroleitos que chegam por dia?
Ver solução completaQuestão 7
Um vendedor de seguros vende em média 3 apólices por semana (7 dias). O número de apólices vendidas pode ser modelada por uma distribuição de Poisson.
- Calcule a probabilidade de que ele venda 2 ou mais apólices numa dada semana;
- Foram escolhidas 4 semanas aleatoriamente, de maneira que se possa supor independência das vendas entre as semanas. Deseja-se saber a probabilidade de em exatamente 3 semanas, entre as 4 escolhidas, terem sido vendidas 2 ou mais apólices;
- Calcule a probabilidade de que ele venda 1 apólice durante um período de 5 dias.
Questão 8
Sabe-se que ocorre, em média, um acidente por dia numa certa estrada. Além disso, o número de ocorrências de acidentes ao longo de um intervalo de tempo de duração fixa segue uma distribuição de Poisson. Calcular a probabilidade de que:
- num determinado dia ocorressem pelo menos 3 acidentes. (calcule o resultado com 2 casas decimais);
- num grupo de 4 dias houvesse exatamente 2 dias, dos 4 selecionados, com pelo menos 3 acidentes por dia.
Obs.: Para simplificar os seus cálculos, use nas contas os valores (aproximados) que constam na tabela abaixo:
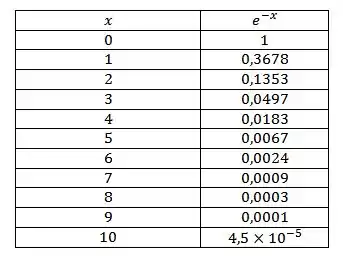
Questão 9
Ocorem, em média, 10 desintegrações por minuto numa amostra de material radioativo. Suponhamos que o número, , de desintegrações por minuto seja uma variável aleatória de Poisson e que seja o intervalo de tempo em minutos entre duas desintegrações sucessivas.
(b) Qual é a probabilidade de que em um intervalo de tempo de 6 segundos não haja desintegrações?
Ver solução completaQuestão 10
Suponha que um livro-texto de 400 páginas apresente um total de 40 erros. Suponha também que os erros estão distribuídos aleatoriamente ao longo do texto. Apresente para cada item uma variável aleatória e um modelo probabilístico adequado para ela. Observe que nos itens (a), (b) e (c) você está modelando uma contagem de eventos em um espaço fixo definido (use Poisson). Calcule a probabilidade de que:
(a) Numa página, aleatoriamente selecionada, não haja erro algum;
(b) Um capítulo de 20 páginas apresente 2 ou mais erros;
(c) Um capítulo de 50 páginas apresente exatamente 3 erros;
(d) Num grupo de 5 capítulos, todos de 20 páginas, exatamente 3 capítulos apresentem 2 ou mais erros.
Ver solução completaQuestão 11
Uma fonte radioativa emite partículas segundo um processo de Poisson com taxa de partículas por segundo. Qual a probabilidade da fonte emitir pelo menos partículas em segundos?
Ver solução completaQuestão 12
a) Se é uma v.a. discreta, descreva o suporte (possíveis valores) de para o caso das seguintes distribuições: Bernoulli, Binomial, Geométrica, Binomial Negativa e Poisson.
Ver solução completaQuestão 13
Suponha que o número de candidatos a participar em determinado curso seja uma v.a. cuja distribuição é uma Poisson com média de 4 inscrições. Se não houver um mínimo de 3 interessados o curso não será oferecido. Por outro lado, na sala há somente 5 computadores e, nas aulas, cada computador será utilizado por apenas um aluno. Calcule a probabilidade:
(a) de que haja mais interessados do que vagas;
(b) de que o curso não seja oferecido por escassez de inscrições (arredonde o resultado para 2 casas decimais);
(c) condicional de que todos os interessados consigam se inscrever dado que foi atingido o número mínimo de inscrições.
(d) de num ano em que houver 6 tentativas independentes de se oferecer este curso, em exatamente 2 delas o curso seja cancelado por escassez de inscrições.
Ver solução completaQuestão 14
Uma fonte radioativa é observada durante intervalos de tempo, cada um de segundos de duração. O número de partículas emitidas , durante cada intervalo, tem uma Distribuição de Poisson com parâmetros partículas/segundo.
- Qual a probabilidade – para um intervalo de tempo – de que ou mais partículas sejam emitidas?
- Qual a probabilidade de que, em pelo menos dos intervalos de tempo, ou mais partículas sejam emitidas?
Questão 15
Estima-se que meteoritos por milhão de atingem a terra anualmente. O número de meteoritos segue uma distribuição de Poisson. A região metropolitana de São Paulo (incluindo o ABC) pode ser aproximada por um quadrado de de perímetro. Calcule a probabilidade de a região ser atingida por um meteorito ao ano.
Ver solução completaQuestão 16
A taxa de ocorrência de crimes em um bairro é de crimes/hora (todos os tempos nessa questão são medidos em hora). A distribuição do número de crimes emum período de tempo é Poisson com parâmetro . A variável aleatória contínua é o instante em que ocorre o primeiro crime a partir do instante , Qual a probabilidade do evento ?.
Ver solução completaQuestão 17
O setor de manutenção de uma empresa consegue atender até 2 casos de quebra de impressoras em um dia ou horas extras serão necessárias naquele dia. A média de quebras é de 2.0 impressoras por dia; a distribuição do número de quebras é Poisson. Qual é a probabilidade de serem necessárias horas extras pelo menos em algum dia da semana de trabalho (5 dias)?
Ver solução completaQuestão 18
Uma empresa faz transporte de material por meio de caminhões e o volume de encomendas que ela recebe oscila ao longo do tempo. Admita que, escolhendo ao acaso um dia de trabalho:
• O número de entregas a serem feitas segue uma distribuição de Poisson com média de 5 entregas/dia;
• A empresa pode contratar, por empreitada, trabalhadores autônomos que constam de uma lista de 6 nomes. Todos eles tem a mesma chance de virem a ser contratados para servir à empresa naquele dia, e há independência entre as decisões de se contratar ou não relativas aos diversos trabalhadores da lista;
• O número de caminhões usados para realizar os serviços naquele dia pode ser igual a: 1 (com probabilidade 0,15), 2 (com probabilidade 0,60), ou 3 (com probabilidade 0,25).
Pergunta-se:
(a) Qual é a probabilidade de que nesse dia sejam feitas no máximo 4 entregas, dado que ocorrerão pelo menos 3 entregas?
Ver solução completaQuestão 19
Suponha que o número de itens que uma loja vende por dia é uma variável aleatória modelada com uma distribuição Poisson, e que sejam vendidos em média 2 itens por dia. Ao longo de trinta dias, pergunta-se:
- Qual o número esperado de itens vendidos ao final dos trinta dias?
- Em aproximadamente em quantos destes trinta dias, a loja irá vender pelo menos um item?
- Em aproximadamente quantos destes trinta dias, a loja irá vender no máximo dois itens?
Questão 20
a) Se é uma v.a. discreta, descreva o suporte (possíveis valores) de para o caso das seguintes distribuições: Bernoulli, Binomial, Geométrica, Binomial Negativa e Poisson.
Ver solução completaQuestão 21
O administrador de um hospital estudou o número de emergências cardíacas diárias no seu hospital, ao longo de vários anos e, concluiu que elas estão distribuídas de acordo com um modelo de Poisson, com média de emergências por dia.
- Qual é a probabilidade de que, num determinado dia, tenha ocorrido mais de emergências?
- Qual é a probabilidade de que, em dois dias, tenham ocorrido, não mais de três emergências?
Questão 22
O pessoal de controle de qualidade afirma que os rolos de fita isolante apresentam, em média, uma emenda a cada 50 metros. Admitindo que a distribuição do número de emendas a cada 50 metros é modelado por uma Poisson, calcule as probabilidades:
- De que não exista nenhuma emenda em um rolo de 125 metros.
- De ocorrerem no máximo duas emendas em um rolo de 125 metros.
- De ocorrer pelo menos uma emenda em um rolo de 100 metros.
Questão 23
Em uma grande rede corporativa de computadores, o número de conexões dos usuários ao sistema pode ser modelado como um processo que segue uma distribuição Poisson com média de 10 conexões por hora. Pergunta-se:
a) Qual a probabilidade de que o intervalo de tempo entre as conexões seja superior a 6 minutos?
b) Qual a probabilidade de que o intervalo de tempo entre conexões esteja entre 2 e 4 minutos?
c) Determine qual é o tempo que no mínimo deve transcorrer para que ocorra uma conexão, com 90% de probabilidade.
Ver solução completaQuestão 24
Se é uma v.a. discreta, descreva o suporte (possíveis valores) de para o caso das seguintes distribuições: Bernoulli, Binomial, Geométrica, Binomial Negativa e Poisson.
Ver solução completaQuestão 25
Suponha que , , sejam variáveis aleatórias independentes, cada uma delas tendo distribuição de Poisson com parâmetro . Faça . Observação: a soma de variáveis aleatórias de Poisson independentes tem distribuição de Poisson.
(b) Calcule o valor exato da probabilidade.
OBS: Aqui se trata de aproximar uma distribuição discreta por uma contínua. Então, da mesma forma como foi visto no caso da aproximação de Binomial por Normal, cabe usar uma correção de continuidade.
Ver solução completaQuestão 26
Numa fábrica de artefatos de porcelana, situada em São Paulo, o processo consiste de duas fases: cozimento e pintura. Na primeira fase, a probabilidade de ocorrência de falhas é de . Na segunda fase, os defeitos ocorrem segundo uma distribuição de Poisson, com parâmetro falhas peças se ocorreu falha na fase de cozimento e com parametro falhas/ peças caso contrário. Se ocorrer defeito em nenhuma ou em apenas uma das fases o produto é vendido por à unidade. Se ocorreu defeito nas duas fases o preço passa a . Qual o valor médio de venda de uma peça?
Ver solução completaQuestão 27
Suponha que o número de passageiros em uma viagem de Uber Juntos, do Fundão à Zona Sul ho horário de retorno, oferecida diariamente pelo motorista Carlos, seja uma v.a que segue uma distribuição de Poisson com média de 2 passageiros interessados. No carro, além do motorista, há somente 4 lugares disponível. Se não houver um mínimo de 3 passageiros, o custo-benefício não é eficiente e neste caso, Carlos não realiza a viagem. Calcule a probabilidade:
- De que, em um determinado dia, tenha mais interessados na viagem de Carlos do que vagas em seu carro;
- De que a viagem não se realize por falta de passageiros interessados (arredonde o resultado para 2 casa decimais);
- De numa semana com 5 dias de tentativas dessas viagem, exatamente 3 delas não tenham sido realizadas por número insuficiente de passageiros. Assuma independência do número de passageiros entre os dias;
- Condicional de que todos os interessados consigam a viagem dado que doi atingido o número mínimo de passageiros.
Questão 28
Uma loja vende em média 3 microcomputadores por dia. Admita que a demanda por este produto segue uma distribuição de Poisson. Ao verificar o estoque, observa-se existirem 2 microcomputadores. Sabe-se que a nova remessa só chegará depois de alguns dias. Qual a probabilidade de que, no fim desse período, a loja não tenha deixado de atender, por falta de estoque, as pessoas que vierem comprar quando:
a) A nova remessa chega em 1 dia?
b) A nova remessa chega em 2 dias?
Suponha que agora esta loja faz parte de uma rede composta por 4 lojas, e que há independência entre as demandas por computadores nas 4 lojas. Em cada uma das lojas há 2 computadores em estoque e a nova remessa chegará em 1 dia. O controlador geral do estoque receberá uma advertência se em pelo menos 2 dessas 4 lojas o estoque não for suficiente para atender a demanada.
c) Qual a probabilidade do controlador receber essa advertência?
Ver solução completaQuestão 29
Seja uma variável aleatória discreta que corresponde à durabilidade de uma peça, em anos incompletos. A função de distribuição acumulada de é dada por:
(a) Determine a função de probabilidade de .
(b) A grandeza é considerada uma característica de qualidade importante do processo de produção. Calcule o valor esperado de .
(c) A durabilidade de uma peça similar produzida por meio de um novo processo de fabricação é . Se é uma Poisson de parâmetro 2, independente de , calcule a probabilidade de que uma peça produzida pelo novo processo dure menos que uma peça produzida pelo processo original, ou seja, .
Ver solução completaQuestão 30
O número de irregularidades por metro quadrado de madeira tem distribuição de poisson com média igual a
Se você comprar de madeira, calcule a probabilidade de você ter no máximo duas irregularidades nessa peça.
Ver solução completaQuestão 31
O número de irregularidades por metro quadrado de madeira tem distribuição de poisson com média igual a
Se você comprar peças de de madeira, calcule a probabilidade de no máximo delas existirem mais de irregularidades
Ver solução completaQuestão 32
O número de irregularidades por metro quadrado de um tecido tem distribuição de poisson com média igual a
Se você comprar de tecido, calcule a probabilidade de você ter no máximo duas irregularidades nessa peça.
Ver solução completaQuestão 33
06) O guarda florestal Pedro sabe que em média ocorrem incêndios florestais acidentais por mês na reserva de que cuida, onde o número de incêndios em um mês segue uma distribuição de Poisson. Além disso, os incêndios em cada mês são independentes entre si. Em cinco meses de observação, qual a probabilidade de ocorrerem incêndios apenas em dos meses?
A)
B)
C)
D)
E)
Ver solução completaQuestão 34
Uma editora verificou que um de seus livros, de páginas, apresentavam erros tipográficos em média. Calcule a probabilidade de um leitor se deparar com mais de erro nas primeiras páginas do livro.
Ver solução completaQuestão 35
Em uma caixa temos moedas, todas independentes e idênticas com probabilidade de cara igual a .
A) A probabilidade de termos exatamente caras se é?
B) A probabilidade de termos exatamente caras se for uma variável aleatória poisson com esperança igual à
Ver solução completaQuestão 36
Você vai fazer uma análise estatística com dados de carros que passam pelas catracas do estacionamento da PUC – Rio. Foram coletados a quantidade, marcas e placas dos veículos que entraram no estacionamento em 1 semana (segunda a sábado; 6 dias).
Considerando somente o último algarismo das placas dos veículos da amostra (0 a 9), responda: (identifique qual é o modelo probabilístico em cada caso).
- Seja o evento: “o terceiro carro a entrar no estacionamento tem final 1 a 3”. Qual a probabilidade deste sucesso acontecer no terceiro carro a entrar no estacionamento?
- Em um determinado período do dia constatou-se que existem somente 20 vagas livres e que nenhum carro iria sair por se tratar de horário de prova. Vinte carros estão na fila para entrar. Qual a probabilidade de menos que 2 carros desta fila serem placa final igual a 3?
- Pelos dados, durante toda a semana (segunda a sábado), passaram pelas catracas 5 carros da marca BMW no estacionamento; ou seja, um evento realmente “raro”. Qual a probabilidade de entrar mais que 2 carros da marca BMW em um dia qualquer da semana?
Questão 37
- Defina um experimento que caracterize uma variável aleatória Poisson. Dê um exemplo real.
Ver solução completaQuestão 38
Um aluno de educação física, conhecido na escola por ser “bom de pontaria”, é desafiado pelos amigos num jogo de basquete. O desafio consiste em fazer 20 lances livres de forma independente ao cesto de basquete e avaliar sua performance nessas jogadas. Sabe-se que em média a cada 20 lançamentos ele acerta 15. Com base nesta informação, responda as perguntas a seguir.
a) Calcule a probabilidade do aluno acertar ao menos 17 das 20 jogadas.
b) Calcule a variância do número de acertos ao cesto nas 20 jogadas.
c) O professor de basquete da escola decide entrar na brincadeira e fazer o desafio. Sabe-se que a probabilidade do professor errar o arremesso ao cesto é de 0,01. Usando a aproximação da Binomial pela Poisson, calcule a probabilidade do professor errar no máximo 2 vezes em 300 lançamentos ao cesto.
Ver solução completaQuestão 39
a) Se é uma v.a. discreta, descreva o suporte (possíveis valores) de para o caso das seguintes distribuições: Bernoulli, Binomial, Geométrica, Binomial Negativa e Poisson.
Ver solução completaQuestão 40
O pessoal de controle de qualidade de uma empresa de asfalto, afirma que uma das rodovias que conecta o Rio de Janeiro com Minas gerais apresenta em média um buraco a cada . Admitindo que a distribuição do número de buracos a cada é modelado por uma distribuição de Poisson, calcule as probabilidades:
- De que não exista nenhum buraco em
- De ocorrerem no máximo dois buracos em
- De ocorrer pelo menos um buraco em
Questão 41
O administrador de um hospital estudou o número de emergências cardíacas diárias no seu hospital, ao longo de vários anos e, conclui que elas estão distribuídas de acordo com um modelo de Poisson, com média de três emergências por dia.
- Qual é a probabilidade de que, num determinado dia, tenha ocorrido, mais de 2 emergências?
- Qual é a probabilidade de que, em dois dias, tenham ocorrido, não mais de três emergências?
Questão 42
- Defina um experimento que caracterize uma variável aleatória Poisson. Dê um exemplo real.
Ver solução completaQuestão 43
a) Se “X” é uma v.a. discreta, descreva o suporte (possíveis valores) de X para o caso das seguintes distribuições: Bernoulli, Binomial, Geométrica, Binomial Negativa e Poisson.
Ver solução completaQuestão 44
O pessoal de controle de qualidade afirma que os rolos de fita isolante apresentam, em média, uma emenda a cada 50 metros. Admitindo que a distribuição do número de emendas a cada 50 metros é modelado por uma Poisson, calcule as probabilidades:
a) De ocorrerem pelo menos duas emendas em um rolo de 125 metros.
b) De ocorrer uma emenda em um rolo de 100 metros.
c) De ocorrerem no máximo duas emendas em um rolo de 150 metros.
Ver solução completa