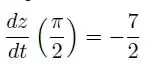Passo 1
O que temos ai é:
Então, pelo caso I da Regra da Cadeia, sabemos que
Então, o que precisamos fazer é calcular cada uma dessas derivadas parciais e depois substituir no ponto .
Passo 2
Vamos começar calcular o correspondente e :
Resolvendo esse sistema temos que
Passo 3
Calcular gradiente da função:
Passo 4
Agora vamos achar as derivadas de e de :
Passo 5
Nossa derivada fica então
Substituindo em e no correspondente:
Resposta
Exercícios de Livros Relacionados
Use a regra da cadeia para achar d z d t ou d w d t . w = x e y z x = t 2 y = 1 - t z = 1 + 2 t
Use a regra da cadeia para determinar d z d t ou d w d t : z = x 2 + y 2 ,x = e 2 t,y = e - 2 t
7-12. Use a Regra da Cadeia para achar ∂ z ∂ s e ∂ z ∂ t .9. z = ln 3 x + 2 y ,x = s ⋅ s e nt , y = t ⋅ cos s
Calcule (d z)/(d t) usando a regra da cadeia:z = y e^x + x e^y , x = cos t , y = sin t .
Seja z = x y , onde x = f ( u ) e y = g ( u ) . Supondo f e g diferenciáveis, f 1 = 2 , g 1 = - 2 , d x d u 1 = - 1 e d y d u 1 = 5 , calcule d z d u ( 1 ) .