Considere um sistema composto por um fio retilíneo infinito e uma espira quadrada de lado . O fio, que está colocado ao longo do eixo de um sistema de referência, é percorrido por uma corrente e gera um campo magnético dado por , onde é a distância até o fio.
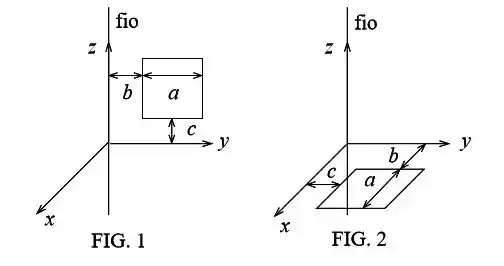
(a) Calcule a indutância mútua entre o fio e a espira quando ela está colocada no plano , conforme a figura .
(b) Calcule a indutância mútua entre o fio e a espira quando ela está colocada no plano , conforme a figura .
(c) Suponha, agora, que a espira tem resistência e que a corrente no fio varia no tempo como , onde é uma constante positiva. Com a espira na posição indicada na figura , calcule a corrente induzida na espira. Esta corrente circula a espira no sentido horário ou anti-horário? Justifique sua resposta.
Passo 1
(a) A autoindutância pode ser achada usando a seguinte expressão:
Para achar o fluxo do campo magnético sobre a espira no plano , usamos:
E então:
Pra achar a autoindutância, então:
Passo 2
(b) Quando a espira está no plano o fluxo magnético é nulo porque o campo magnético é perpendicular ao vetor área, ou seja, não há passagem de linhas de campo magnético através da superfície que é circulada pela espira. Portanto, a indutância é nula.
Passo 3
(c) A corrente induzida na espira quando ela está no plano é
Podemos calcular a força eletromotriz induzida pela seguinte expressão(análoga à diferença de potencial de um indutor):
Substituindo:
Fazendo a derivada da expressão para a corrente:
Pela lei de Lenz, como o fluxo aumenta no tempo, a corrente tem que gerar um fluxo que contrapõe esse aumento, logo, o sentido da corrente é anti-horário.
Resposta
a)
b)
c) , no sentido anti-horário.