Exercícios de Indutores e Indutância - Lista de Exercícios Resolvida
Questão 1
Um anel condutor de raio está no plano e centrado na origem de um sistema de coordenadas. Outro anel condutor , concêntrico a possui raio , conforme a figura.
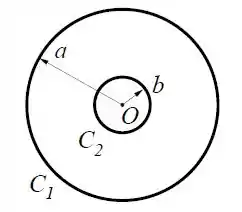
Calcule a indutância mútua entra os dois anéis. Justifique as aproximações feitas.
No anel circula uma corrente . Calcule a força eletromotriz induzida no anel 1 pelo anel 2.
Dado: O campo magnético no centro de um anel de raio por onde passa uma corrente é .
Ver solução completaQuestão 2
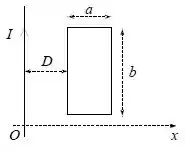
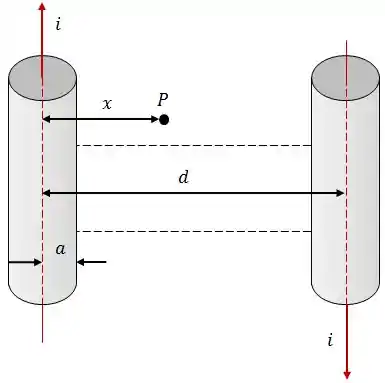
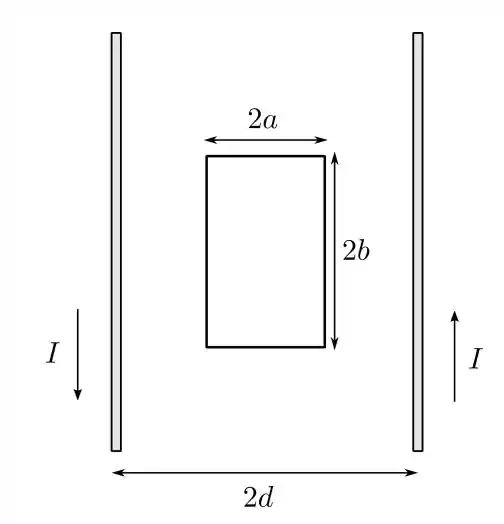
Dois fios longos e paralelos, cada um de raio , cujos centros estão separados por uma distância , são percorridos por corrente iguais , mas de sentidos opostos, conforme a figura.
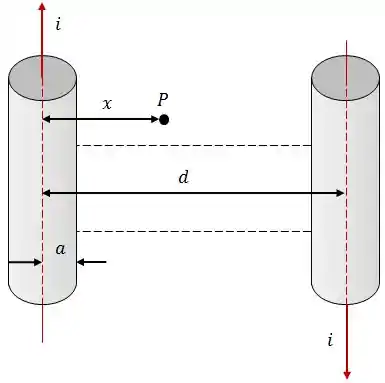
Calcule:
- O módulo, a direção e o sentido do campo magnético , no ponto , devido aos fios.
- O fluxo magnético através de um retângulo formado pelas linhas tracejadas e os dois lados externos dos fios. Considere um comprimento e despreze o fluxo dentro dos fios.
- A indutância para este par de fios.
Questão 3
Em um certo instante a corrente e a força eletromotriz auto-induzida em um indutor têm os sentidos indicados na figura abaixo.
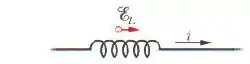
A corrente está aumentando ou diminuindo?
A força eletromotriz induzida é e a taxa de variação da corrente é . Determine a indutância.
Ver solução completaQuestão 4
Um solenoide circular ideal, muito longo, tem número de espiras , raio e comprimento . Se alterarmos o raio e o número de espiras de tal solenoide, para o dobro e a metade, respectivamente, mantendo seu comprimento inalterado, o que ocorre com a sua autoindutância? Considere que o solenoide é muito longo (“infinito”): .
- Aumenta
- Diminui
- Depende da corrente que passa no solenoide
- Não se altera
Questão 5
Seja um solenoide longo, formado por um enrolamento de espiras circulares. Considere as seguintes três afirmativas sobre sua autoindutância: (I) ela é proporcional ao quadrado do raio das espiras; (II) ela é proporcional à taxa de variação da corrente no solenoide, e (III) ela é proporcional à corrente que circula no solenoide. Assinale a opção que indica qual(is) dessas afirmativas está(ão) correta(s).
- Nenhuma
- Apenas a I
- Apenas a II
- Apenas a III
- Apenas a I e a II
- Apenas a I e a III
- Apenas a II e a III
- Todas
Questão 6
Dois solenóides fazem parte do circuito de ignição de um automóvel. Quando a corrente em um dos solenóides diminui de para zero em uma força eletromotriz de é induzida no outro solenóide.
Qual é a indutância mútua dos solenóides?
Ver solução completaQuestão 7
Considere um solenoide ideal de raio e uma espira circular de raio coaxial a ele, e suponha que (ou seja, a espira está fora do solenoide).
Pelo solenoide passa uma corrente não-estacionária . Denotando a indutância mútua do sistema por , as autoindutâncias do solenoide e da espira por e , e o campo produzido pelo solenoide em seu exterior por , qual das afirmações abaixo é verdadeira?
pois .
depende de .
pois .
depende de .
depende de .
depende de .
Ver solução completaQuestão 8
Um indutor de conduz uma corrente de . Qual deve ser a taxa de variação da corrente para que a força eletromotriz no indutor seja ?
Ver solução completaQuestão 9
A indutância de uma bobina compacta de espiras é . Calcule o fluxo magnético através da bobina quando a corrente é .
Ver solução completaQuestão 10
Uma bobina circular tem de raio e espiras compactas. Um campo magnético externo de módulo é aplicado perpendicularmente ao plano da bobina.
Se a corrente na bobina é zero, qual é o fluxo magnético que enlaça as espiras?
Quando a corrente na bobina é em um certo sentido, o fluxo magnético através da bobina é zero. Qual é a indutância da bobina.
Ver solução completaQuestão 11
Um capacitor de fica completamente carregado quando conectado a uma bateria de . Depois disso, desliga-se a bateria e liga-se o capacitor carregado a um indutor de . A máxima corrente que passa pelo indutor é aproximadamente:
- ;
- ;
- ;
- ;
- ;
Questão 12
Uma espira retangular está no mesmo plano de um fio longo retilíneo que conduz uma corrente . A espira tem um comprimento (paralelo ao fio) e largura , conforme figura. A indutância mútua do sistema dobrará em qual (is) dos seguintes casos?
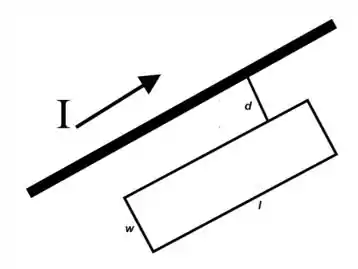
- Dobrando-se .
- Dobrando-se
- Dobrando-se .
- Reduzindo-se pela metade.
- II e III;
- I, III e IV;
- I, II, III e IV;
- Somente I;
- Somente III.
Questão 13
Considere um solenoide ideal de autoindutância , comprimento e com espiras. Ao montar-se um novo solenoide com um fio maior, de modo que ele tenha o dobro de espiras e o dobro do comprimento, qual será a autoindutância desse novo solenoide?
Ver solução completa
Questão 14
Um indutor de indutância e um indutor de indutância são ligados em paralelo. Quando a taxa de variação da corrente no indutor maior é , a taxa de variação da corrente no indutor menor é:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 15
Um anel condutor de raio está no plano e centrado na origem de um sistema de coordenadas. Outro anel condutor , concêntrico a possui raio , conforme a figura.
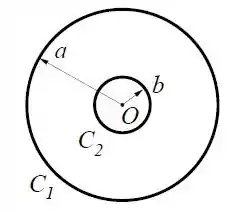
Calcule a indutância mútua entra os dois anéis. Justifique as aproximações feitas.
No anel circula uma corrente . Calcule a força eletromotriz induzida no anel 1 pelo anel 2.
Dado: O campo magnético no centro de um anel de raio por onde passa uma corrente é .
Ver solução completaQuestão 16
PARTE 2:
Um indutor de indutância é percorrido por uma corrente variável no tempo, gerada por uma fonte externa e dada pela função: para ( em segundos e em ).
Qual o maior módulo da fem induzida, no intervalo considerado?
Em qual instante de tempo a fem induzida inverte sem sentido?
Em qual intervalo de tempo a fem induzida e a corrente aplicada possuem o mesmo sentido?
Ver solução completaQuestão 17
Considere um fio infinito percorrido por uma corrente estacionária . Coplanar com o fio está uma espira retangular de lados e e resistência . A distância da espira ao fio infinito é D, conforme a figura.
Dado: O módulo do campo magnético produzido por um fio infinito num ponto a uma distância do fio é .
Calcule o fluxo magnético sobre a área da espira.
Calcule a mútua indutância do sistema fio-espira.
Suponha que a espira é deslocada com velocidade constante paralelamente ao fio. Calcule o valor da corrente na espira.
Suponha que a espira é afastada do fio com velocidade na direção perpendicular a esse fio. Calcule a força eletromotriz induzida e a corrente na espira no instante em que a distância da espira ao fio é . Determine o sentido da corrente induzida (horário ou anti-horário), justificando sua resposta.
Ver solução completaQuestão 18
Considere um sistema composto por um fio retilíneo infinito e uma espira quadrada de lado . O fio, que está colocado ao longo do eixo de um sistema de referência, é percorrido por uma corrente e gera um campo magnético dado por , onde é a distância até o fio.
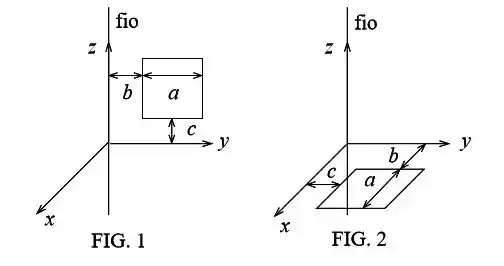
(a) Calcule a indutância mútua entre o fio e a espira quando ela está colocada no plano , conforme a figura .
(b) Calcule a indutância mútua entre o fio e a espira quando ela está colocada no plano , conforme a figura .
(c) Suponha, agora, que a espira tem resistência e que a corrente no fio varia no tempo como , onde é uma constante positiva. Com a espira na posição indicada na figura , calcule a corrente induzida na espira. Esta corrente circula a espira no sentido horário ou anti-horário? Justifique sua resposta.
Ver solução completaQuestão 19
Uma espira quadrada condutora de lado e resistência está orientada paralelamente a um fio condutor infinito a uma distância .
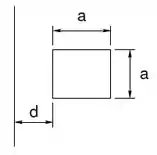
(a) Calcule a indutância mútua do sistema.
(b) Se o fio infinito é percorrido de baixo para cima por uma corrente , onde é o tempo e é uma constante positiva, calcule a corrente induzida na espira quadrada. Determine e explique o sentido da corrente induzida.
Ver solução completaQuestão 20
Um solenoide muito longo, coaxial com o eixo , tem comprimento , raio e espiras no total. O solenoide é colocado no vácuo. Desprezando efeitos de borda, o campo dentro do solenoide é , onde é a corrente através das espiras.
(a) (1,0 ponto) Calcula a indutância do solenoide.
(b) (1,5 ponto) Uma corrente variável no tempo dada por percorre o solenoide. Usando a lei de Faraday, calcule o vetor campo elétrico na região , onde é a distância ao eixo do solenoide.
Ver solução completaQuestão 21
Seja um solenoide longo, formado por um enrolamento de espiras circulares. Considere as seguintes três afirmativas sobre sua autoindutância: (I) ela é proporcional ao quadrado do raio das espiras; (II) ela é proporcional à taxa de variação da corrente no solenoide, e (III) ela é proporcional à corrente que circula no solenoide. Assinale a opção que indica qual(is) dessas afirmativas está(ão) correta(s).
- Nenhuma
- Apenas a I
- Apenas a II
- Apenas a III
- Apenas a I e a II
- Apenas a I e a III
- Apenas a II e a III
- Todas
Questão 22
Considere um solenoide ideal de raio e uma espira circular de raio coaxial a ele, e suponha que (ou seja, a espira está fora do solenoide).
Pelo solenoide passa uma corrente não-estacionária . Denotando a indutância mútua do sistema por , as autoindutâncias do solenoide e da espira por e , e o campo produzido pelo solenoide em seu exterior por , qual das afirmações abaixo é verdadeira?
pois .
depende de .
pois .
depende de .
depende de .
depende de .
Ver solução completaQuestão 23
Em certo instante, a corrente e a força eletromotriz induzida em um indutor têm os sentidos indicados na figura. Neste instante, o valor da força eletromotriz induzida é de e o módulo da taxa de variação da corrente é de . Determine o valor da indutância e diga se a corrente está aumentando ou diminuindo no indutor.
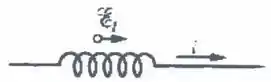
(a) , diminuindo.
(b) , diminuindo.
(c) , aumentando.
(d) , aumentando.
(e) , diminuindo.
Ver solução completaQuestão 24
Um solenóide de indutância conduz uma corrente constante . Esta corrente é reduzida para , a uma taxa constante, no intervalo de tempo de . O valor absoluto da força eletromotriz no solenoide é:
Questão 25
A figura abaixo mostra um fio condutor retilíneo, conduzindo uma corrente
O fio é coplanar a uma bobina retangular com espiras compactas. A bobina possui resistência . O fluxo do campo magnético gerado pelo fio através de uma espira da bobina é dado por , onde não depende do tempo.
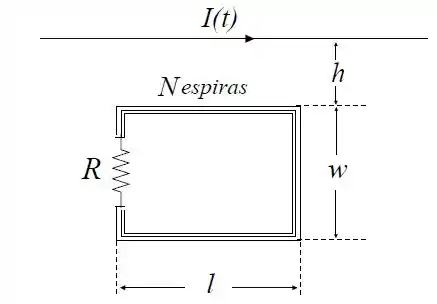
Obtenha a indutância mútua do sistema fio e bobina em função de e .
Ver solução completaQuestão 26
Dois fios longos e paralelos, cada um de raio , cujos centros estão separados por uma distância , são percorridos por corrente iguais , mas de sentidos opostos, conforme a figura.
Calcule:
- O módulo, a direção e o sentido do campo magnético , no ponto , devido aos fios.
- O fluxo magnético através de um retângulo formado pelas linhas tracejadas e os dois lados externos dos fios. Considere um comprimento e despreze o fluxo dentro dos fios.
- A indutância para este par de fios.
Questão 27
Um solenoide longo de comprimento e raio tem um enrolamento com espiras. O módulo do campo no interior do solenoide é .
- Calcule a auto-indutância do solenoide.
- Repita o cálculo do item (a) para o caso em que o solenoide está preenchido com um material de suscetibilidade .
Questão 28
Um anel e raio é colocado concentricamente em um solenoide muito longo de espiras, comprimento e diâmetro . Qual a indutância mútua quando ?
- Nenhuma das alternativas listadas
Questão 29
Uma bobina circular tem de raio e espiras compactas. Um campo magnético externo de módulo é aplicado perpendicularmente ao plano da bobina. (a) Se a corrente na bobina é zero, qual é o fluxo magnético que enlaça as espiras? (b) Quando a corrente na bobina é em um certo sentido, o fluxo magnético através da bobina é zero. Qual a indutância da bobina?
Ver solução completaQuestão 30
Num circuito com a corrente em função do tempo é dada por , onde é dado em segundo, em ampères e o ângulo de fase em radianos.
Quando, após , a corrente atingirá seu valor máximo?
Qual é a indutância?
Ver solução completaQuestão 31
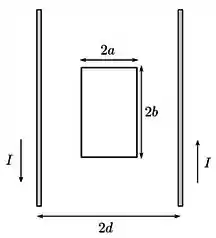
Uma espira condutora retangular de lados e é posicionada no mesmo plano que um par de fios condutores finos, retilíneos, infinitos e paralelos, como mostrado na figura abaixo. Os fios transportam correntes estacionárias de mesma intensidade e sentidos opostos e estão separados por uma distância , como indicado. O centro da espira está equidistante dos fios e os lados de comprimento são paralelos a eles. Determine a indutância mútua entre a espira e o par de fios.
Questão 32
Parte :
Considere um solenóide ideal de espiras, raio e comprimento transportando uma corrente no sentido indicado pela figura abaixo. O campo magnético em seu interior é dado por .
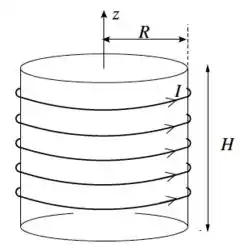
- Determine a auto-indutância do solenóide.
- Considere, agora, que a corrente elétrica seja variável no tempo , sendo uma constante. Determine o vetor campo elétrico induzido nas regiões (dentro do solenóide) e (fora do solenóide).
Questão 33
Um solenóide toroidal tem seção transversal quadrada, raio interno , raio externo e voltas de um fio condutor fino enroladas de forma compacta em torno dele. Qual é a auto indutância deste solenóide?
Questão 34
Duas bobinas são mantidas fixas no espaço. Quando a corrente na bobina 1 é zero e a corrente na bobina 2 aumenta à taxa de , a força eletromotriz na bobina 1 é . (a) Qual é a indutância mútua das duas bobinas? (b) Quando a corrente na bobina 2 é zero e a corrente na bobina 1 é , qual é o enlaçamento de fluxo da bobina 2?
Ver solução completaQuestão 35
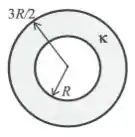
- Deduza a expressão da capacitância deste capacitor. Expresse seu resultado em termos de , e . Atenção: não use expressão “memorizada” para .
- Calcule a carga elétrica livre sobre a parede condutora interna de raio Expresse seu resultado em termos de , , e .
- Calcule a carga elétrica induzida na substância não condutora, nas proximidades da parede interna de raio . Expresse seu resultado em termos de , , e .
Questão 36
Um solenoide circular ideal, muito longo, tem número de espiras , raio e comprimento . Se alterarmos o raio e o número de espiras de tal solenoide, para o dobro e a metade, respectivamente, mantendo seu comprimento inalterado, o que ocorre com a sua autoindutância? Considere que o solenoide é muito longo (“infinito”): .
- Aumenta
- Diminui
- Depende da corrente que passa no solenoide
- Não se altera
Questão 37
O diagrama abaixo mostra a direção da induzida em um indutor, que é a parte de um circuito maior. Qual das afirmações sobre este indutor é correta?
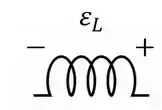
(a) A corrente é constante e aponta para direita
(b) A corrente é constante e aponta para esquerda
(c) A corrente está aumentando e aponta parar a esquerda
(d) A corrente está diminuindo e aponta para a direita
(e) A corrente está aumentando e aponta para direita
Ver solução completaQuestão 38
Considere um solenóide toroidal de seção transversal de raio . Ele é atravessado por uma corrente de intensidade que varia lentamente com o tempo. Considere também três espiras orientadas paralelamente às seções transversais do solenoide: , uma espira circular de raio , , uma espira triangular de lados iguais a e , uma espira quadrada de lado , dispostas no solenóide como mostrado na figura abaixo, envoltas e centralizadas no mesmo. Sejam , e as indutâncias mútuas entre o solenóide e as espiras , e , respectivamente, quando consideradas individualmente. Nessa situação, podemos afirmar que:
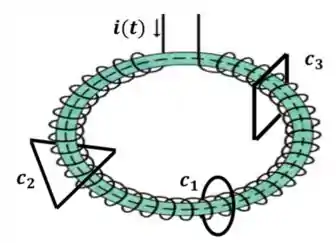
Questão 39
Uma espira condutora retangular de lados e é posicionada no mesmo plano que um par de fios condutores finos, retilíneos e paralelos, como mostrado na figura abaixo. Os fios transportam correntes estacionárias de mesma intensidade e sentidos opostos e estão separadas por uma distância , como indicado. O centro da espira está equidistante dos fios e os lados de comprimento são paralelos a eles. Determine a indutância mútua entre a espira e o par de fios.
Questão 40
Dizemos que dois indutores de auto-indutâncias e e indutância mútua desprezível estão ligados em série quando uma mesma corrente atravessa os dois.
Calcule a diferença de potencial entre os terminais de associação. Expresse-a em termos de e e a taxa de variação de com o tempo .
Ver solução completaQuestão 41
Dizemos que dois indutores de auto-indutância e e indutância mútua desprezível estão ligados em paralelo quando eles estão submetidos à mesma diferença de potencial elétrico .
Calcule a taxa de variação da corrente total com o tempo. Expresse-a em termos de , e .
Ver solução completaQuestão 42
Dizemos que dois indutores de auto-indutância e e indutância mútua desprezível estão ligados em paralelo quando eles estão submetidos à mesma diferença de potencial elétrico .
Mostre que esse arranjo pode ser substituído por um único indutor equivalente de auto-indutância e determine em termos de e .
Ver solução completaQuestão 43
Dizemos que dois indutores de auto-indutâncias e e indutância mútua desprezível estão ligados em série quando uma mesma corrente atravessa os dois.
Mostre que esse arranjo pode ser substituído por um único indutor equivalente de auto-indutância e determine em termos de e .
Ver solução completaQuestão 44
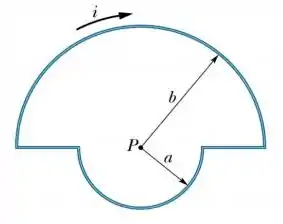
- Calcule o vetor campo magnético produzido por um longo fio condutor, de diâmetro desprezível, que repousa no eixo dos de um sistema de coordenadas cartesianas, e que transporta uma corrente sentido positivo do eixo dos .
- Uma corrente circula em uma espira formada por dois segmentos radiais e duas semicircunferências de raios e com um centro comum no ponto (veja figura abaixo). Calcule o módulo e o sentido (para dentro ou para fora da página) do vetor campo magnético no ponto .
- Calcule o módulo e o sentido do vetor momento magnético da espira
Questão 45
Um solenoide longo de comprimento e raio tem um enrolamento com espiras.
Calcule a autoindutância do solenoide. Calcule a energia armazenada no solenoide quando pelo fio circula uma corrente .
Dado: o campo magnético no interior do solenoide é . Ignore a variação do campo próximo às extremidades do solenoide.
Repita os cálculos do item (a) para o caso em que o solenoide está preenchido com um material de suscetibilidade .
Ver solução completaQuestão 46
Deseja-se fazer um resistor na forma de uma mola enrolando um fio em torno de um cilindro isolante. Para tornar o valor da indutância o menor possível podemos:
- Enrolar o fio com o maior número possível de volta.
- Fazer nenhuma das afirmações listadas.
- Enrolar metade do fio em metade do cilindro e a outra metade do fio na outra metade do cilindro.
- Enrolar metade do fio em um sentido e a outra metade do fio em sentido contrário sobre a camada anterior.
Questão 47
Uma espira condutora quadrada de lado e a resistência está orientada paralelamente a um fio condutor infinito percorrido por uma corrente , a uma distância .
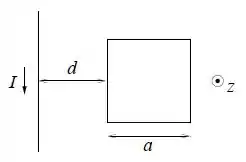
- Calcule a indutância mútua do sistema. Escolha a normal à espira no sentido positivo do eixo . Obs: o campo magnético a uma distância de um fio infinito percorrido por uma corrente é .
- Para com , calcule a corrente induzida na espira quadrada e determinar seu sentido. (justifique a sua resposta)
Questão 48
Uma bobina toroidal de raio interno e seção reta quadrada de lado , com , possui espiras percorridas por uma corrente .
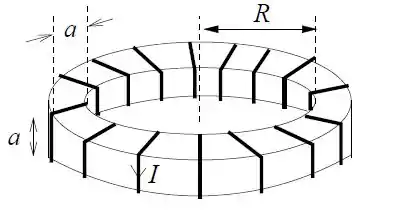
Calcule o vetor campo magnético no interior do toróide.
Calcule a autoindutância da bobina supondo que o módulo do campo magnético seja aproximadamente constante dentro da bobina.
Suponha que a bobina toroidal seja preenchida com um núcleo de um material magnético com permeabilidade magnética relativa . Calcule os novos valores do vetor campo magnético no seu interior e da autoindutância.
Ver solução completaQuestão 49
Um circuito que contém um indutor funciona a uma frequência de . A tensão de pico é e a corrente de pico no indutor é . Qual é a indutância do indutor?
- ;
- ;
- ;
- ;
- ;
Questão 50
Um circuito com resistência , contido no plano , é constituído por dois arcos de circunferência com raios e e por dois segmentos retos. Este circuito envolve um solenoide muito longo, com eixo paralelo ao eixo , espiras por unidade de comprimento e raio tal que , conforme a figura. Pelo solenoide passa uma corrente que flui no sentido anti-horário. cresce com o tempo com taxa . Desprezando efeitos de borda, a intensidade do campo magnético no interior do solenoide é .
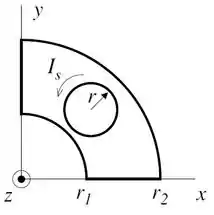
(a) (1,0 ponto) Calcule o fluxo do campo do solenoide através do circuito.
(b) (1,0 ponto) Calcule o coeficiente de mútua indutância entre o solenoide e o circuito.
(c) (1,0 ponto) Calcule o sentido (horário ou anti-horário) e a magnitude da corrente induzida no circuito.
Ver solução completaQuestão 51
A figura abaixo mostra duas espiras condutoras circulares, concêntricas e coplanares. A espira menor possui raio e transporta uma corrente estacionária de intensidade no sentido indicado, enquanto a espira maior possui raio e transporta uma corrente estacionária de intensidade no sentido oposto.
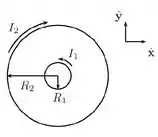
- Determine o campo magnético resultante produzido pelas duas espiras no centro delas.
- Suponha agora que , de forma que podemos considerar que o campo magnético produzido pela espira maior é constante em todos os pontos dentro da espira menor e tem o valor calculado no centro. Nessa situação, determine a indutância mútua entre este par de espiras.
Questão 52
Um solenoide circular ideal tem número de espiras , raio e comprimento . Se alterarmos o raio e o número de espiras de tal solenoide, para o triplo e a metade, respectivamente, mantendo seu comprimento inalterado, o que ocorre com a sua auto-indutância? Considere que o solenoide é muito longo (“infinito”): .
(a) Aumenta.
(b) Depende da corrente que passa no solenoide.
(c) Diminui.
(d) Não se altera.
Ver solução completaQuestão 53
2.8) Considere um cilindro oco de raio interno , raio externo e comprimento . O cilindro,
feito de material isolante, possui uma densidade de carga uniformemente distribuída em
seu corpo. Calcule o momento de dipolo magnético gerado pela rotação desse cilindro em torno do seu eixo longitudinal. Considere que o cilindro gira com frequência angular .
Ver solução completa