A figura abaixo mostra duas espiras condutoras circulares, concêntricas e coplanares. A espira menor possui raio e transporta uma corrente estacionária de intensidade no sentido indicado, enquanto a espira maior possui raio e transporta uma corrente estacionária de intensidade no sentido oposto.
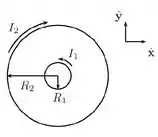
- Determine o campo magnético resultante produzido pelas duas espiras no centro delas.
- Suponha agora que , de forma que podemos considerar que o campo magnético produzido pela espira maior é constante em todos os pontos dentro da espira menor e tem o valor calculado no centro. Nessa situação, determine a indutância mútua entre este par de espiras.
Passo 1
a) O campo magnético gerado pela corrente em seu centro vale
em que, pela regra da mão direita, o campo está entrando no plano da página e é perpendicular a ela.
Para a corrente , o campo será
que está saindo do plano da página. Portanto, o campo magnético resultante no centro das espiras será dado por
Passo 2
b) Para calcularmos a indutância mútua, precisamos saber como é o fluxo do campo magnético através da área da superfície da espira interna.
Como o problema diz que , isso significa que podemos considerar que o campo magnético tem praticamente o mesmo valor em todos os pontos da espira menor de raio . Essa informação é que nos permite colocar para fora da integral no cálculo do fluxo magnético que faremos abaixo...
Como está entrando no plano da página, podemos colocar o elemento de área apontando para dentro da superfície da espira interna. Portanto, isso vai dar o seguinte
Agora, aplicando a definição de indutância mútua , teremos