- Calcule , onde é o sólido limitado por , , , e .
Passo 1
Cara, em exercícios como esse, sempre vamos começar desenhando a região . Mas não se desespere porque basta seguir o enunciado do problema e ir limitando o sólido, saca?
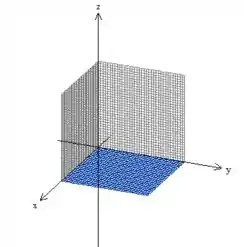
Nesse caso aqui mesmo, o problema nos fala que o sólido está limitado pelos planos coordenados , e :
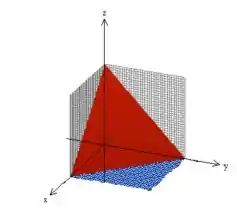
Mas o sólido também está delimitado por esse plano aqui . Não se preocupe se você não sabe desenhar esse plano direitinho, basta que saiba que ele, por ter seus termos positivos, tem esse aspecto aqui ohh
Porém, esse tetraedro vermelho também está delimitado por mais uma superfície:
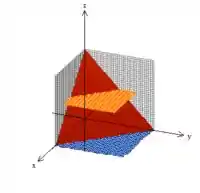
Passo 2
Não trabalhamos com esse sólido dessa forma, por isso, a ideia aqui sempre será partir para a descrição dele. Nesse caso, cabe o , onde temos o variando de uma “base” até um “teto”.
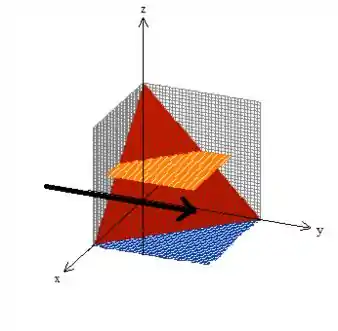
(DICA: acompanhe a seta preta para você ver experimentalmente quem é a base quem é o teto)
Como o plano vermelho é justamente o plano , basta que isolemos o ...
Quanto ao e ao , olhemos para a projeção do sólido no plano . Bora?
Passo 3
Pow! Relaxa! Projetar esse sólido nesse plano nada mais é do que olhar para o sólido
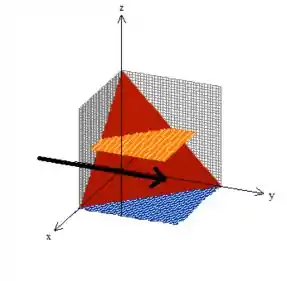
mas dessa vez, vai ser de ladinho, como se colocássemos o olho em cima do eixo e vesse pra lá:
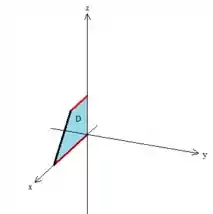
Note que essa reta em preto escuro ali, é justamente a reta em que o plano toca o pano , por isso , e a reta: ...
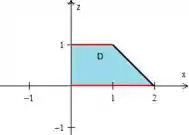
Descrever e é apenas descrever essa região aí, que pode ser feita também utilizando a região :
- varia em um intervalo numérico:
- , entre funções:
como a reta preta ...
Passo 4
Bem, agora é só montar a integral tripla e correr para o abraço!
Lembre-se que na integral mais interna, fica a que tem mais variável, no caso o , seguido pelo e depois o :
Começando com a integral de dentro...
substituindo os limites de integração em ...
integrando e substituindo os limites em ...
eliminando esses parêntesis...
concluímos que o resultado da integral é...