- Calcule , onde é o tetraedro limitado pelos planos coordenados e pelo plano
Passo 1
Cara, em exercícios como esse, sempre vamos começar desenhando a região . Mas não se desespere porque basta seguir o enunciado do problema e ir limitando o sólido, saca?
Nesse caso aqui mesmo, o problema nos fala que o sólido está limitado pelos planos coordenados:
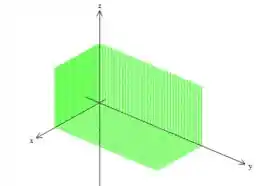
Mas o sólido também está delimitado por esse plano aqui . Não se preocupe se você não sabe desenhar esse plano direitinho, basta que saiba que ele, por ter seus termos positivos, tem esse aspecto aqui ohh
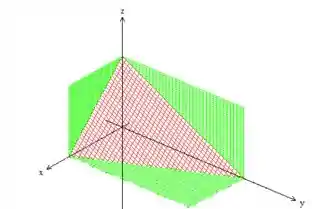
delimitando justamente o tetraedro do enunciado, pegou?:)
Passo 2
Não trabalhamos com esse sólido dessa forma, por isso, a ideia aqui sempre será partir para a descrição dele. Nesse caso, cabe o , onde temos o variando de uma “base” até um “teto”
Como o plano vermelho é justamente o plano , basta que isolemos o ...
Quanto ao e ao , olhemos para a projeção do sólido no plano . Bora?
Passo 3
Pow! Relaxa! Projetar esse sólido nesse plano nada mais é do que olhar para o sólido
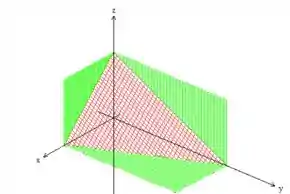
mas dessa vez, de cima para baixo:
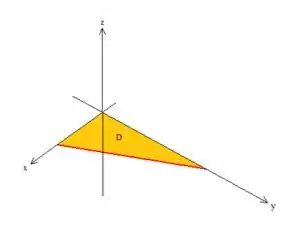
Note que essa reta em vermelho escuro ali, é justamente a reta em que o plano toca o pano , ou o , então...
Essa reta passa justamente por quando é , como pode ser reparado.
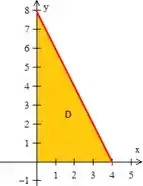
Descrever e é apenas descrever essa região aí, que pode ser feita também utilizando a região :
- varia em um intervalo numérico:
- , entre funções:
Passo 4
Bem, agora é só montar a integral tripla e correr para o abraço!
Lembre-se que na integral mais interna, fica a que tem mais variável, no caso o , seguido pelo e depois o :
Começando com a integral de dentro...
é tomado como uma constante perante a integral em , então...
Substituindo os limites em ...
E agora integrando em (tomando o cuidado com novamente, afinal ele ainda é considerado como uma constante)
Substituindo em
e dando aquela simplificada marota
obtemos