. Seja a região sólida no primeiro octante limitada pelos planos , e pelo cilindro . Calcule
Passo 1
Vamos dar uma olhadinha no nosso sólido:
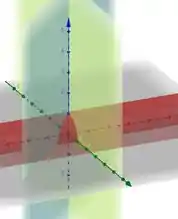
Ou seja, o nosso sólido é aquela partezinha no primeiro octante entre os planos, e se projetarmos no plano teremos um triângulo retângulo abaixo:
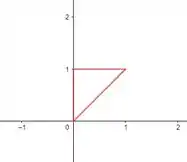
E podemos ver que essa região está em e , agora temos todas as bases para desenvolver a questão.
Passo 2
Com as informações que mostramos no passo anterior podemos já definir o nosso sólido pois sabemos que o sólido está limitado superiormente pelo cilindro, então:
Ou seja: