Seja o tetraedro sólido com vértices .
a) Encontre a equação do plano que passa pelos pontos .
b) Calcule a integral tripla
Passo 1
a) Oi! Tá bem? Para montar a equação de um plano, a gente precisa de duas coisas. A primeira é um vetor normal a esse plano .
E para achar esse cara, vamos calcular dois vetores, paralelos a esse plano, formados por esses 3 pontos que temos. Só fazer um ponto menos o outro. Ficam assim:
Agora a gente vai achar nosso vetor normal ao plano a partir desses dois.
A gente tinha dois vetores paralelos ao plano. Se a gente calcular o produto vetorial entre eles, isso nos dá um vetor normal a esses dois vetores, e logo, um vetor normal ao plano.
Passo 2
Aí para achar a equação do plano que passa por esses pontos, a gente precisa usar a fórmulinha:
Onde é um vetor normal ao nosso plano. Que a gente já achou.
E é um ponto que pertence ao plano. Podemos escolher qualquer um dos nossos 3 pontos. Aí podemos escrever:
Nossa fórmulinha fica:
Passo 3
b) Queremos calcular a integral tripla
Onde é o tetraedro de vértices . A gente precisa descrever essa região usando extremos de integração para poder calcular a integral.
Vamos esboçar esse cara, é só marcar esses pontos no gráfico e os ligar por retas, assim:
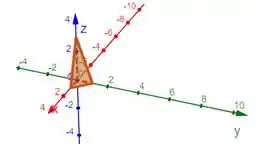
Aí a gente percebe que no eixo , nossa região está acima de e abaixo do plano que passa pelos pontos . A gente descobriu a equação desse cara!
Podemos então dizer que
Passo 4
Falta limitar e . Agora repara que no plano , a projeção da nossa região é o triângulo de vértices
Olha a cara dele:
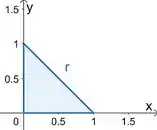
O que a gente precisa fazer aqui é definir essa região como extremos de integração.
Passo 5
Precisamos limitar uma das variáveis entre constantes e a outra pode estar entre funções, beleza?
Vamos começar olhando para o eixo . A gente pode dizer que nele, a nossa região está limitada entre os valores de e .
Agora olhando para , a gente vê que ele está entre a reta , limitando nossa região por cima, e a reta , limitando nossa região por baixo. Então a genta pode escrever:
A reta é a reta que passa pelos pontos e . Podemos usar a equação da reta para acha-la. Fica assim:
Aí a nosso precisa estar limitado entre constantes ou funções de , aí fica assim:
Passo 6
Agora é montar a integral.
Temos os extremos de integração:
Aí como precisamos integrar primeiro em relação a variável que está entre funções de e , e depois a que está entre funções de , fica assim:
Passo 7
Calculando essa belezura:
Resposta
a)
b)