Calcule o volume do sólido contido no primeiro octante (i.e., ) e limitado pelas superfícies e .
Passo 1
Vamos começar desenhando esse sólido, para poder montar o problema. Temos dois paraboloides, um virado para cima e um para baixo, dessa forma:
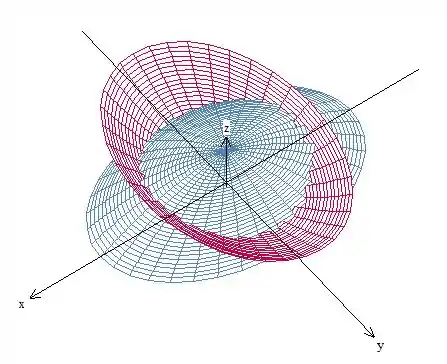
A região do problema é a que fica entre as duas superfícies, contida no primeiro octante.
Passo 2
Agora vamos escrever matematicamente essa região. Podemos dizer que varia entre as duas superfícies, enquanto as variáveis e pertencem a um domínio do plano , a projeção do sólido (no caso, um círculo).
Assim, a região é a seguinte:
Passo 3
Beleza, agora vamos levar isso para a integral
Passo 4
Agora nós vamos escrever essa região plana . Antes de tudo, vamos descobrir que círculo é esse fazendo a intersecção entre as duas superfícies:
A região é, então, o interior dessa circunferência de raio . Vamos usar coordenadas polares então:
Como o enunciado pede a região no primeiro octante apenas, podemos escrever:
Passo 5
Levando para a integral a mudança polar:
Agora é só resolver isso aí!