Sendo o sólido limitado pelo cilindro e pelos planos , e no primeiro octante, com função densidade , determine sua massa
Passo 1
O problema pede que calculemos a massa do sólido delimitado pelas superfícies acima, sabendo que sua densidade é dada por . Nós sabemos que:
Onde é o diferencial de massa e o de volume. Integrando ambos os lados na região em que o sólido está contido, temos que:
Vamos fazer um esboço dessa região :
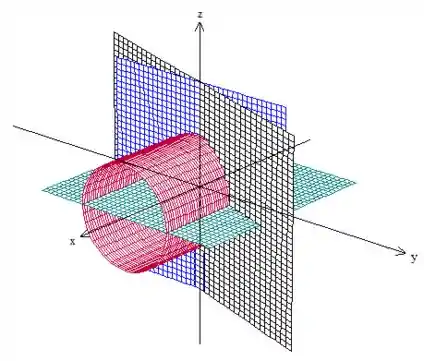
Fazendo os cortes no primeiro octante, temos isso aqui:
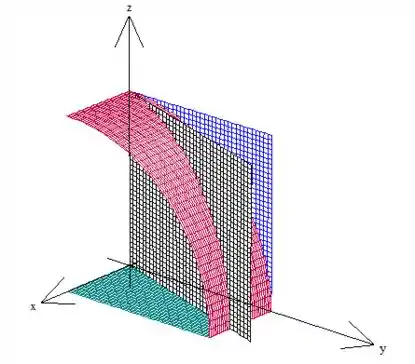
Como varia entre a equação dos planos e e temos, no plano , uma projeção do sólido que representa um domínio (um setor de círculo), vamos descrever essa região como tipo III.
Passo 2
A projeção do sólido no plano é esse setor aqui:
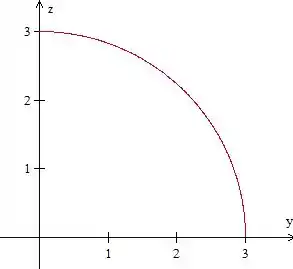
Com raio porque o cilindro possui raio .
A melhor forma de descrever essa área, é por meio de coordenadas polares, fazendo:
Teremos:
Passo 3
Vamos agora substituir os intervalos que encontramos nas integrais iteradas. Como tivemos que fazer uma mudança de variáveis para descrever o domínio , vamos escrevê-lo depois da primeira integração, para não gerar confusões. Temos:
Passo 4
Integrando em relação a , temos:
Passo 5
Agora sim, vamos substituir os intervalos de e fazer a substituição polar.
Você poderia ter feito isso antes, sem problemas. Optamos por fazer assim apenas por questão de organização.
Passo 6
Agora, integramos em relação a :
Passo 7
Agora, nós fazemos o seguinte:
Então, vamos a substituição
Aplicando na integral