Seja o tetraetro sólido com vértices .
- Encontre a equação do plano que passa pelos pontos .
- Calcule a integral tripla
Passo 1
Fala povo, tudo bem? Olha só a macete bacana: 3 pontos definem um plano. Ok, ok, mas e daí? Bem, sabe o que também da pra fazer com 3 pontos? Duas retas! Sendo assim, podemos dar nome aos bois:
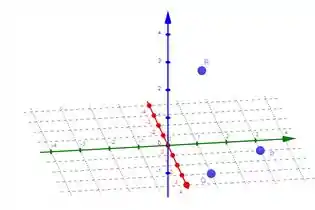
Basta montarmos vetores com esses pontos de forma que um desses pontos seja comum aos dois vetores. Escolhendo como ponto em comum, temos:
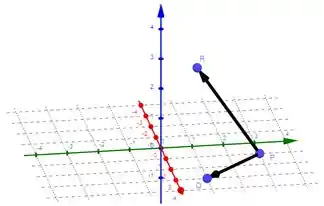
Como que isso ajuda em algo, você deve estar se perguntando. Bem, lembre-se que a equação geral de um plano é:
Onde é um ponto pertencente ao plano e é a direção do vetor normal ao plano. Galera, ai que entra o pulo do gato! Se e são coplanares, então um vetor perpendicular a eles será normal ao plano! Pra achar esse vetor, fazemos o produto vetorial:
Calculando essa determinante, temos:
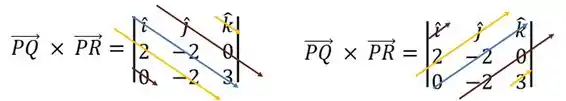
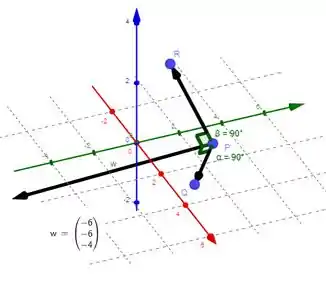
Usando o ponto e as direções do vetor , chegamos na seguinte equação do plano:
O que é o mesmo que:
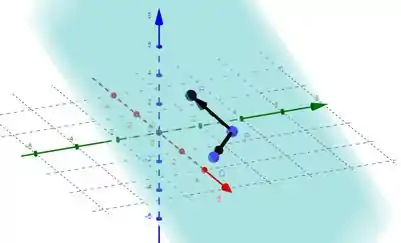
Passo 2
Show, pra fechar essa questão, vamos calcular sabendo que é um tetraedro cheio de pontinhos. Pegando todos os pontos do enunciado, podemos esboçar esse tetraedro:
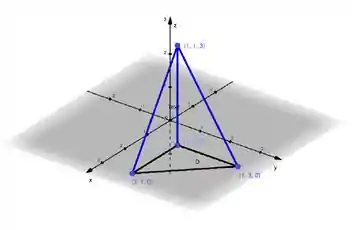
Se juntarmos essa imagem com a do plano, vemos que uma das fazes do tetraedro está inteiramente contida no plano:
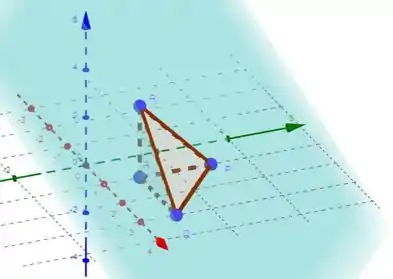
O que mostra pra gente que o nosso limite de integração de deve ser:
Isolando na equação do plano, temos:
Logo:
Já os limites de integração de a gente tira olhando a base do tetraedro do plano :
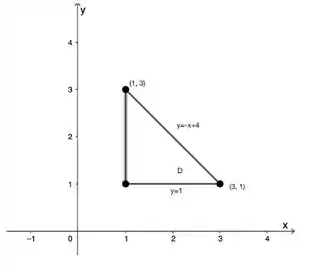
Onde a reta pode ser obtida fazendo um sistema de equações que inclua os pontos e :
Equação menos equação resulta em:
Jogando esse valor de em qualquer uma das duas equações, encontramos . Sendo assim, pelo desenho, concluímos que:
E a integral fica:
Passo 3
Bora fechar essa questão e partir pro abraço! Agora é só integrar! Pra começar, vamos fazer a integral mais interna:
Pra ela, nada mais é do que uma constante! Logo:
A integral tripla vira então uma integral dupla:
Novamente, a gente pega a integral mais interna, que é em função de . Podemos ainda, pra enrolar menos, separar ela em três:
Pra primeira, temos:
Pra segunda, temos:
Pra terceira, temos:
Juntando as três, temos:
O que, juntando termos em comum, resulta em:
Ufa, quase lá! Pra fechar, a gente vai remontar e integral, que vai ganhar a forma final de:
E agora é só integrar normal em relação a ! Vamos ter:
Continuando a simplificação, chegamos a: