UFABC-Função de várias variáveis - Lista 7 integrais triplas
Faça um esboço do solido cujo o volume é dado pelas integrais abaixo e calcule tais integrais.
Passo 1
Bem pessoas, essa é uma questão quase padrão de integração tripla. Ele deu a integral bonitinha, mas precisamos montar a superfície, dessa vez não tem como fugir, portanto precisamos montar para após isso resolver.
Mas como resolver? Bem, para resolver precisaremos de alguns conceitos de matemática básica e também de conceitos de integração.
Você lembra deles?
CAAAAAAAAAAAAALMA, se lembrar ótimo. Caso contrário vamos resolver aqui passo a passo com você para você aprender certinho belezinha?
Então vaaaaaaaaaaaamos lá
Passo 2
Amigão para resolver isso aqui primeiramente vamos precisar identificar uma coisa, o eixo está cartesiano enquanto os demais estão polares. Isso indica que possivelmente esse solido está em coordenadas cilíndricas e por isso aquele e apenas a jacobiana.
Analisando o nosso problema temos que teta varia de até . Logo, temos que o nosso domínio polar é de uma circunferência.
Agora falta apenas o eixo , o eixo que é a equação de um cilindro, sendo assim temos que a nossa superfície deve ser algo mais ou manos assim:
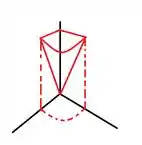
Passo 3
Agora vamos para a parte mais chatinha que é resolver as integrais, eeeeeeeentão vamos lá.
Primeiro resolvendo da integral mais interna:
Vemos que nosso problema não depende da variável nos domínios de integração, então podemos resolver ela logo e deixar da seguinte forma:
Realizando a distributiva e fazendo as integrações temos que: