- Calcule , onde é o sólido limitado pelos planos , , , e .
Passo 1
Bem a primeira coisa que devemos fazer aqui é tentar entender um pouco mais sobre esse sólido . E não há nada melhor pra entendê-lo do que o desenhando no espaço. Bora?
Devemos começar desenhando cada uma dessas superfícies, vamos começar aqui limitando o primeiro octante com essas superfícies: , , .
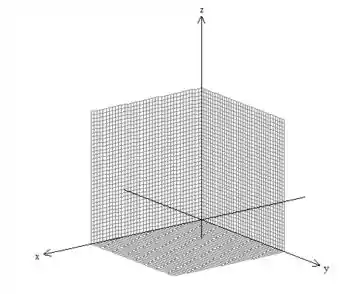
Agora, essa superfície , desenhamos um pouco diferente. Acompanhe-me!
Passo 2
Para superfície que só dependem de duas incógnitas como , podemos sempre desenha-la no plano primeiro. No nosso caso, , note no plano nos representa uma reta e que vou desenha-la aqui pra você ohhh:
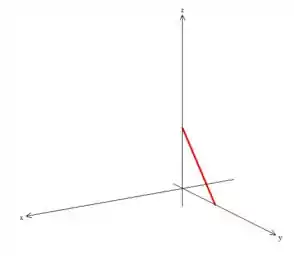
Pois bem! Agora como essa equação não depende de , o que deve ser feito é “puxar” essa reta aí em torno do eixo , saca? Então essa é a superfície:

No caso... É um plano !
Passo 3
Novamente, podemos repetir o processo para a outra reta: .
Desenhando então no plano , essa reta
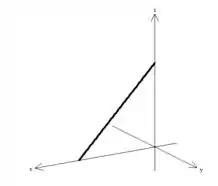
e a puxando, obteremos
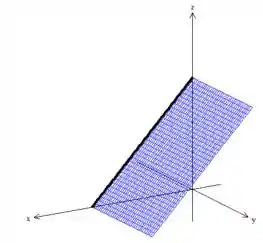
que somado as outras superfícies nos dá
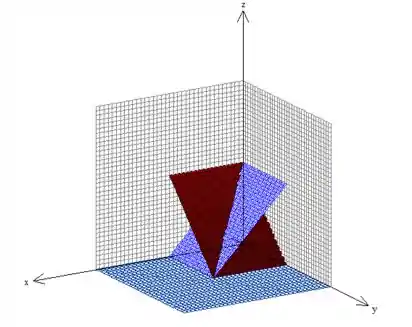
o nosso tão esperado sólido , percebeu? (ele é esse pedacinho de pirâmide )
Passo 4
Não trabalhamos com esse sólido dessa forma, por isso, a ideia aqui sempre será partir para a descrição dele. Nesse caso, cabe o , onde temos o variando de uma “base” até um “teto”.
(DICA: acompanhe a seta preta para você ver experimentalmente quem é a base quem é o teto)
Como o plano vermelho é justamente o plano , basta que isolemos o ...
Quanto ao e ao , olhemos para a projeção do sólido no plano . Bora?
Passo 5
Pow! Relaxa! Projetar esse sólido nesse plano nada mais é do que olhar para o sólido
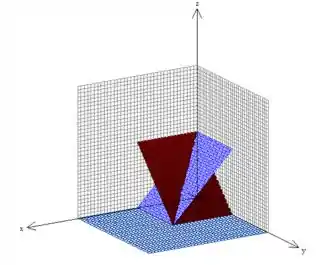
mas dessa vez, vai ser de ladinho, como se colocássemos o olho em cima do eixo e vesse pra lá:
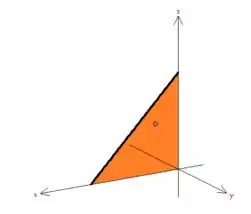
Note que essa reta em preto escuro ali, é justamente a reta em que o plano toca o pano .
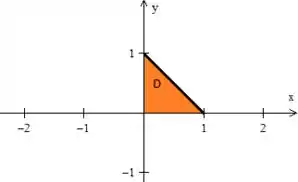
Descrever e é apenas descrever essa região aí, que pode ser feita também utilizando a região :
- varia em um intervalo numérico:
- , entre funções:
como a reta preta ...
Passo 6
Bem, agora é só montar a integral tripla e correr para o abraço!
Lembre-se que na integral mais interna, fica a que tem mais variável, no caso o , seguido pelo e depois o :
Começando com a integral de dentro...
substituindo os limites de integração em ...
integrando e substituindo os limites em ...
obtemos essa integral nada bonita. Mas!!! antes de sairmos calculando igual maluco esse quadrado e cubo aí, experimentemos uma mudança de variável...
não se esqueça de mudar os limites também
substituindo...
Repare que esse limite está invertido. Podemos revertê-lo caso trocamos o sinal da integral...
dando no final: