Calcule o volume do sólido limitado pelas superfícies , .
Passo 1
O volume desse sólido, que chamaremos de , é dado pela seguinte integral:
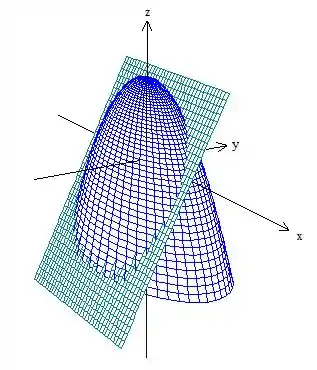
Vamos começar fazendo um esboço dessa região. Temos um paraboloide elíptico virado para baixo cortado por um plano perpendicular ao :
Passo 2
Vamos escrever essa região como tipo I, limitando entre as equações do plano e do paraboloide. Sendo a projeção da região no plano , temos o seguinte:
Levando isso para a integral, temos:
Passo 3
Integrando em relação a :
Passo 4
Agora vamos descrever essa região , projeção do sólido no plano .
Primeiro vamos descobrir a equação da curva que limita , fazendo a interseção entre a equação do plano e a do paraboloide:
Mexendo um pouco nisso aqui, temos:
Então, sabemos que é o interior dessa elipse deslocada da origem no plano :
Vamos, então, usar coordenadas elípticas deslocadas, ok:
Esse coeficiente adicionado às coordenadas polares está aí para cancelar os coeficientes da elipse, “transformando” ela numa circunferência descrita por .
Então, é descrita por e . Fazendo a mudança polar na integral, temos:
Passo 5
Agora vamos integrar isso aí:
Agora, em relação a :