Considere a região no primeiro octante delimitada pelo plano e pelo paraboloide .
- Descreva a região delimitada.
- Calcule o volume dessa região.
Passo 1
Letra a)
Bem, vamos começar desenhando essa região ai, para entender melhor o problema. Temos um paraboloide virado para baixo (em vermelho), limitado ao primeiro octante (planos em verde) e cortado pelo plano (em azul).
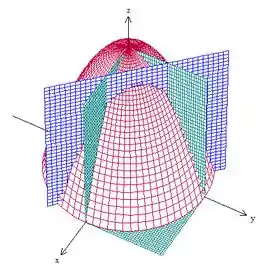
Para você visualizar melhor, a região é essa aqui:
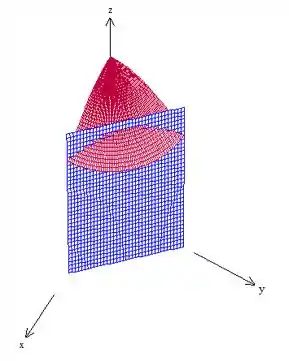
Beleza?
Passo 2
Como podemos ver, no plano , temos um domínio . Em , o sólido é limitado embaixo pelo plano e em cima pelo outro plano paraboloide. Vamos, então, escrever essa região como tipo I.
Temos a coordenada variando desde até a superfície do paraboloide , logo, . Logo, a região pode ser escrita como:
Passo 3
Vendo a região de cima, podemos descobrir seu domínio , que, no caso, é o seguinte triângulo:
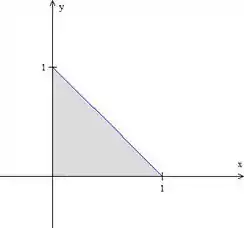
Essa reta azul é onde o plano corta o plano . Portanto, sua equação é a própria equação do plano fazendo , .
Podemos dizer, então, que varia desde até a equação da reta , enquanto varia desde até .
Temos, então:
Portanto,
Passo 4
Letra b)
Bom, o volume desse sólido será , certo?
Vamos agora substituir os intervalos que encontramos na integral iterada:
Cuidado com a ordem dos diferenciais! Ela tem que obedecer a ordem dos intervalos nas integrais. Lembre-se de que o último intervalo (o de fora) dever ser sempre um número.
Passo 5
Integrando em relação a , temos:
Passo 6
Agora, integramos em relação a :
Passo 7
Finamente, integramos em relação a :