Encontre o volume da região limitada pelas superfícies e .
Passo 1
As duas superfícies dadas no enunciado são paraboloides. Mas perceba que a primeira superfície:
Tem abertura para cima (quando e aumentam, o também aumenta). Já a segunda tem abertura para baixo:
Vamos fazer um esboço dessas superfícies:
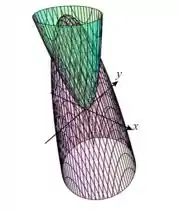
Beleza, nosso objetivo é calcular o volume entre essas superfícies. V
Passo 2
As superfícies se encontram de forma bem confusa, vamos tentar encontrar isso algebricamente. Precisamos igualar as duas equações:
Isso que nós achamos é como se fosse uma “sombra” (no plano) da intersecção das duas superfícies! Dá uma olhada nesse desenho porque é importante que isso fique bem claro:
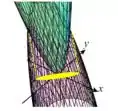
Essa elipse amarela está totalmente contida no plano , e é só a sombra da interseção entre as duas superfícies. A interseção em si é bem mais complicada e irregular do que isso.
Mas pra que precisamos dessa sombra? Isso é bem comum em questões desse tipo, porque todos os pontos do volume que queremos calcular estão “acima” dessa sombra. Essa região vai definir os limites de integração para o e para o !
Passo 3
Então tá, como achamos os limites do e do a partir dessa equação de elipse. Vamos desenhar ela no plano :
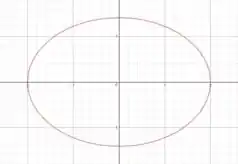
Achar os extremos do é mais fácil, basta pegar os pontos em que :
Então nosso vai variar nesse intervalo:
E para cada um desses valores de , como fica o ? Ah, agora é só isolar na equação da elipse?
E então nosso varia nesse intervalo aqui:
Beleza, agora só falta descobrir como o varia para cada um desses pares !
Passo 4
Vamos olhar de novo para a imagem:
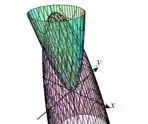
Nossa integral já está ali andando em toda a região imediatamente abaixo do volume que queremos calcular. Mas agora falta dizer pra ela o seguinte: qual é a “altura” que ela tem que calcular em cada ponto !
Mas isso é tranquilo: como queremos o volume “entre” a superfície esverdeada e a superfície avermelhada, é só mandarmos a integral ir da “altura” (coordenada ) de uma até a outra!
Agora já estamos prontos para substituir tudo na integral!
Passo 5
Juntando tudo o que calculamos, descobrimos que o volume pode ser calculado por essa integral aqui:
Uma integral bastante feia, né? Mas é mais fácil do que parece! Começamos integrando em relação a , como não tem nada na integral:
Agora vamos integrar isso em relação a . Só pra não ficar confuso, vamos fazer a integral indefinida antes, e depois substituímos com os limites de integração:
Beleza? Agora nós vamos substituir aqueles limites nessa expressão:
Bastante confuso! Mas agora vamos poder somar os termos:
Vamos colocar o em evidência no :
E agora vamos multiplicar esse mesmo por , de forma que ele fique igual àquele termo que está na raiz!
Ok, agora podemos juntar esses termos iguais, lembrando que uma raiz quadrada é o mesmo que um expoente :
E agora resolvendo aquela diferença de frações:
E agora chegamos em uma integral mais razoável:
O próximo passo é resolvê-la!
Passo 6
Nós conhecemos bem a cara dessa integral:
Ela está pedindo uma substituição trigonométrica! Lembre que quando temos um termo do tipo , devemos usar a substituição , então:
E vamos trocar também os limites de integração:
Jogando isso tudo na integral (vamos simplificar as constantes de uma vez):
Vamos tirar essas constantes:
E agora podemos calcular essa constante em uma calculadora e juntar os cossenos:
Agora sim, chegamos na última integral!
Passo 7
Para evitar uma grande confusão, vamos simplesmente calcular essa integral indefinida:
E depois usamos esse resultado para calcular a integral que queremos. Lembra como se calcula a integral quando temos uma potência par do cosseno?
E agora aplicamos a integral por partes. A fórmula (que normalmente se usa) é essa aqui:
Aplicando isso no nosso caso com , isso quer dizer que:
Então:
E vamos precisar usar uma identidade trigonométrica para resolver a integral da direita:
Assim:
Agora sim, sabemos resolver aquela integral da direita:
E finalmente:
Passo 8
Agora o último passo (prometo):
Já sabemos calcular essa integral, vamos só substituir os limites de integração e multiplicar pela constante:
Como o é zero e também:
Então:
Finalmente! Conseguimos!
Resposta
O volume da região é .