A integral que expressa o cálculo da massa do sólido limitado pelos planos , de densidade é:
Passo 1
É legal começarmos observando essas superfícies que estamos trabalhando.
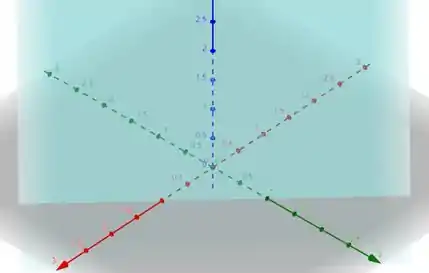
Primeiro, pra identificarmos onde o está variando, que seria da base (plano ), até bater no plano azul. Isolamos ele.
Entçao, logo de cara já temos que o varia entre (passado pelo encunciado) e .
Passo 2
Para identificarmos agora a variação de devemos observar a projeção no plano ou seja, justamente quando temos .
Isolando então o
Já quanto a , observa que o máximo que ele assume é 1. Ou seja
Passo 3
Juntando tudo oque temos então já conseguimos montar a integral, e ficamos então com: