- Use uma integral tripla para calcular o volume do sólido limitado por:
-
, , , .
Passo 1
Cara! Calculo de volume a esse altura do campeonato pra gente é uma integral tripla de :
Não temos uma boa visualização desse sólido por isso sempre é bom começar por aqui
Relaxa, pois fazer isso nada mais é do que desenhar todas essas superfícies aí ao mesmo tempo! Mas aqui, para você entender perfeitamente, primeiro vamos considerar cada uma delas separadas, ok?
Comecemos com as duas mais simples: e . São dois planos paralelos ao ( é o próprio )
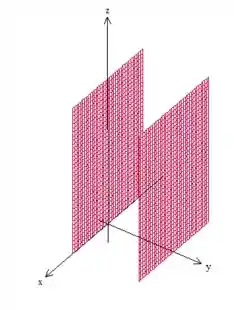
Quanto a esse outro plano aqui , venha comigo!
Passo 2
Para superfície que só dependem de duas incógnitas como , podemos sempre desenha-la no plano primeiro. No nosso caso, , no plano nos representa uma reta
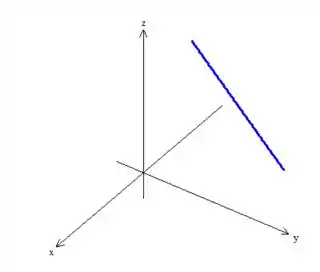
Pois bem! Agora como essa equação não depende de , o que deve ser feito é “puxar” essa reta aí em torno do eixo , saca? Então essa é a superfície:
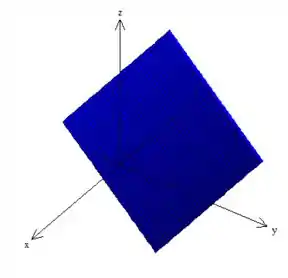
Passo 3
A última superfície, , encontra-se da mesma forma que a anterior, afinal de contas ele só depende de duas variáveis:
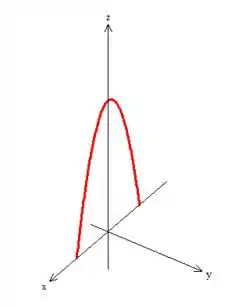

Passo 4
Wooooow! Cuidado, pois ainda não terminamos de ver o sólido! Temos que colocar essas coisas juntas
Assim, o nosso sólido é...
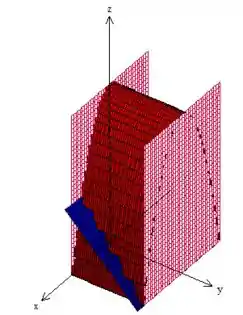
Para você por dentro, vou tirar esse plano da frente, veja:
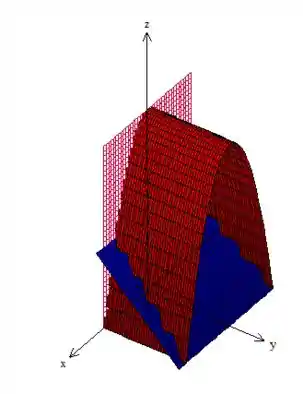
O sólido é esse que esta indo do plano azul e indo até o “teto” vermelho
Passo 5
Não trabalhamos com esse sólido dessa forma, por isso, a ideia aqui sempre será partir para a descrição dele. Nesse caso, cabe o , onde temos o variando de uma “base” até um “teto”
Como o plano azul é justamente o plano , isolando ...
o cilindro vermelho é ...
Quanto ao e ao , olhemos para a projeção do sólido no plano . Bora?
Passo 6
Pow, relaxa! Projetar esse sólido nesse plano nada mais é do que olhar para o sólido
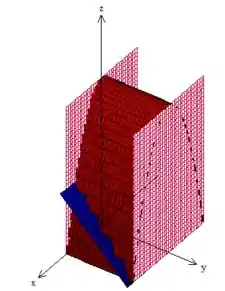
mas dessa vez, de cima para baixo:
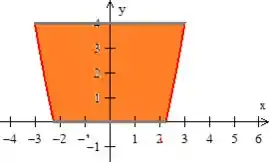
Podemos descrever essa projeção como uma região do , afinal, já sabemos que
Falta agora obtermos a variação do . Pelo desenho da projeção, o está variando desse pedacinho vermelho até o outro. Agora quem são essas curvas?
Se olharmos para o sólido, vamos notar que essas curvas são sombras da intercessão do plano azul, com esse cilindro bizarro vermelho. Fazer essa interação na matemática é resolver os sisteminha entre a equação do plano azul com o cilindro, vermelho:
Como queremos a variação do , isolemos nessa equação...
Logo...
Passo 7
Bem, agora é só montar a integral tripla e correr para o abraço!
Lembre-se que na integral mais interna, fica a que tem mais variável, no caso o , seguido pelo e depois o :
Começando com a integral de dentro...
Resposta
![]()