A figura abaixo ilustra um corpo de massa pendurado no teto de um trem bala por
um fio inextensível de comprimento . Quando o trem possui aceleração, o pêndulo
se encontra inclinado, fazendo um ângulo com a vertical. Pode-se provar que, se é
a aceleração da gravidade local, então . Como temos que , onde a função é a função inversa da
tangente. Supondo que , resolva os itens seguintes.
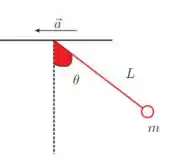
(a) Sabendo que , encontre
e
(b) Se a aceleração do trem tomar valores cada vez maiores, o ângulo se aproxima de que valor? E se , então tende para algum número?
(c) Faça um esboço dos gráficos de , com suas
assíntotas.
Passo 1
Fala galera, tudo beleza? vamos para mais uma questão de Cálculo 1. Como de costume, vamos anotar as informações importantes do enunciado. Sabemos que:
Vamos começar resolvendo a letra a)
Passo 2
A letra a quer saber quais são
e
Como achamos isso?

Bem vamos começar escrevendo a definição de dentro do limite. Dessa forma temos:
pela linearidade do limite
pela definição da tangente
Então precisamos estudar o comportamento de quando nos aproximamos pela direita. Mas o que aproximar pela direita significa mesmo?

Significa que estamos olhando o comportamento da função perto de olhando apenas os valores maiores que . E de modo análogo definimos aproximar pela esquerda, olhando os valores menores que .
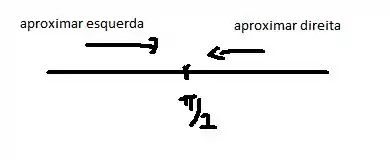
Agora podemos analisar nossa função.
Quando temos que e
Então
Vamos analisar
Assim como no caso anterior, temos que:
Quando temos que e
Então
Um jeito menos algébrico de verificar esses limites é utilizar o ciclo trigonométrico para vermos o comportamento da tangente:
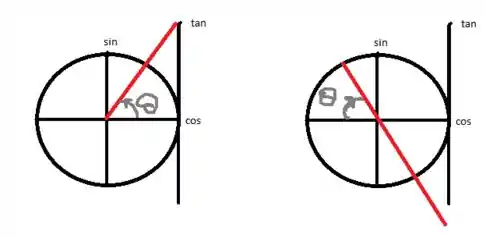
Passo 3
Agora vamos fazer a letra b)
Assim como na letra a), agora queremos saber o comportamento assintótico de para valores de aceleração altos () e baixos () . Como fazemos isso?

O enunciado nos diz que é para uma dada aceleração, então podemos usar essa função. Só relembrando que essa função é dada por:
Como não temos o costume de usar a função arco-tangente ela parece ser assustadora, mas podemos torná-la bem simples com a seguinte interpretação:
O é o ângulo cuja tangente é
Bem mais simples né?

Agora podemos calcular os limites de interesse:
Que limite é esse? Qual é o ângulo cuja tangente é infinita?
Usando o resultado da letra a), vemos que esse ângulo é
De forma análoga, calculamos
Que limite é esse? Qual é o ângulo cuja tangente é menos infinito?
Usando o resultado da letra a), vemos que esse ângulo é
Passo 4
Para finalizar a questão, só nos resta responder a letra c)

Nosso objetivo é fazer um esboço dos gráficos de e de .
Vamos começar com gráfico de
pelo enunciado, sabemos que:
então seu gráfico é parecido com o gráfico da tangente, mas seus valores são 10 vezes maiores. Então o gráfico fica:
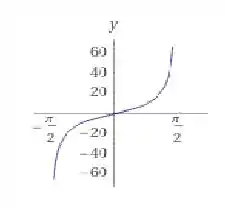
Mas e o gráfico de ? Como é a função inversa de , seu gráfico será a reflexão do gráfico de sobre a reta
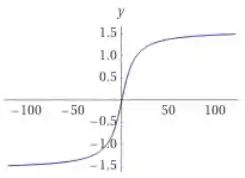

Prontinho pessoal. Com isso terminamos mais uma questão de Calculo 1, espero que os passos tenham ficado claros. Até a próxima!!!
Resposta
Ei, a resposta está no passo a passo :)