Seja dada por
a) Calcule e
b) Determine os valores de para que a equação admita exatamente duas soluções reais distintas.
Passo 1
Faaaala galera da USP... vamos matar essa juntos?

Nessa questão, temos uma função e queremos calcular o limite dela, para tendendo a zero lateralmente a para tendendo ao infinito.
Começando por , substituindo os valores teremos:
E zero mais infinito, é puramente mais infinito, portanto:
Passo 2
Agora, queremos calcular
Que é uma indeterminação...
Podemos então aplicar no termo , para isso fazemos:
Dessa forma, temos:
E pela propriedade de logaritmo, temos que a subtração de logaritmo é igual ao logaritmo da divisão:
Como a função é uma função contínua, podemos aplicar:
E o limite de com tendendo a infinito resulta em:
Por l’hospital, podemos derivar em cima em baixo:
Portanto, temos:
Passo 3
Para finalizar, queremos encontrar os valores de cuja qual a função resulta em dois valores distintos.
Vamos reparar no seguinte...
A função é definida apenas para valores . Isso acontece por que a função só permite positivo e diferente de zero.
E nós já calculamos o limite dessa função nas extremidades desse intervalo.
Ou seja, essa é uma função que apresenta uma assíntota vertical em e que vai pra infinito quando vai para infinito. Ela faz algo mais ou menos assim.
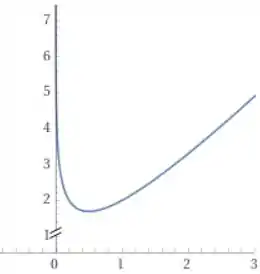
Para que a equação possua duas soluções distintas, é necessário que seja um valor que esteja acima desse mínimo da função.
Vou como exemplo colocar aqui um qualquer que tem duas soluções distintas.
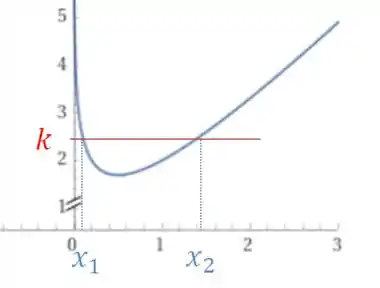
Nesse exemplo acima, e são as soluções distintas para a equação .
Beleza, precisamos então encontrar o mínimo dessa função e para isso, vamos deriva-la e igualar a zero.
E substituindo na função teremos:
Aqui, podemos aplicar novamente as propriedades de logaritmo:
E lembrar que , afinal , portanto:
Portanto, para todo a equação admite duas soluções distintas.
Resposta
a)
b)