UFF, Niterói - Campus da Praia Vermelha, Cálculo IA, Provas de C1 - Profº Leonardo - VE1 - 2023.1, Questão 3b
3. Seja , uma função contínua em todo seu domínio ou . Sobre se sabe:
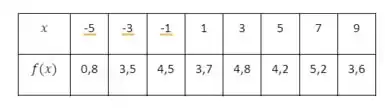
b) Se, além da tabela acima, também souber que
como isso afeta, se é que afeta, suas conclusões sobre o número garantido de soluções da equação ?
Passo 1
Os limites laterais de em estão dados como:
Isso significa que está se aproximando de 4.2 à medida que se aproxima de 0 tanto pelo lado esquerdo quanto pelo lado direito. Esses limites indicam que é contínua em e que o valor de em é igual a 4.2.
Vamos agora analisar a tabela de valores dada e considerar as informações adicionais dos limites:
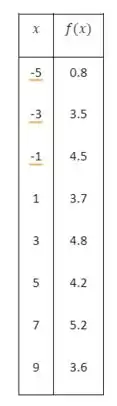
Passo 2
Agora, sabemos que , o que significa que a função atinge o valor 4.2 no ponto . Além disso, os valores da função nos pontos vizinhos de estão próximos de 4.2. Isso nos leva a concluir que a função passa por 4.2 em uma região em torno de .
Considerando o comportamento da função nos pontos vizinhos de e que ela é contínua em , podemos concluir que a função deve cruzar a linha em .
Portanto, a função tem pelo menos quatro soluções para a equação , sendo uma delas em . A informa��ão adicional dos limites em afeta as conclusões, aumentando o número garantido de soluções da equação .
Resposta
Portanto, a função tem pelo menos quatro soluções para a equação , sendo uma delas em . A informação adicional dos limites em afeta as conclusões, aumentando o número garantido de soluções da equação .