USP – Física 1 – 2020 – P-SUB – Discursiva
Q - Uma bola de tênis de e com velocidade inicial colide com uma parede e retorna com velocidade de mesmo valor em módulo. A figura abaixo representa a força da parede sobre a bola durante a colisão. Sabendo-se que o tempo que dura a colisão entre a bola e a parede é , o máximo valor da força que a parede exerce sobre a bola durante a colisão, em Newtons, é:
• Considere a bola como uma partícula de massa .
Passo 1
Vem comigo que a gente resolve essa juntos!
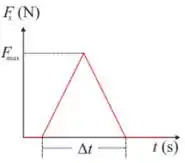
O gráfico do enunciado nos mostra o comportamento da força da parede sobre a bola durante o tempo. Desse gráfico podemos tirar o módulo do impulso que a parede realizou na bola, que vai ser igual a área do gráfico, então:
Agora para achar o valor de vamos usar o teorema do impulso-momento, que diz que o impulso da força resultante que atua em um corpo é igual a variação de momento desse corpo, então:
Onde é o vetor momento linear depois da colisão e é o vetor momento linear antes da colisão.
Vamos então atrás dos momentos e depois podemos encontrar o valor da força máxima.
Passo 2
O vetor momento inicial é dado por:
Já que , onde estamos fazendo por enquanto .
O vetor do momento final é o seguinte:
Mas segundo enunciado a bola retorna da colisão com a parede com o mesmo módulo, mas consequentemente com sentido diferente, então:
Com isso temos que:
Passo 3
Então usando o fato de que:
Tomando o módulo, temos:
Logo:
Substituindo os valores que temos, ficamos com:
Então temos que:
Então fechamos essa com sucesso!