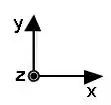
Um bate-estaca de gravidade funciona com um princípio muito simples. Um martelo de massa é solto do repouso a uma altura acima de uma estaca de massa . A colisão dura um intervalo de tempo muito curto . Imediatamente após a colisão o martelo e a estaca adquirem a mesma velocidade e chegam ao repouso, depois de afundarem uma distância . Suponha o intervalo de tempo de afundamento como sendo . Todo movimento acontece ao longo da direção vertical. Utilize o sistema de coordenadas abaixo, dê suas respostas em função dos dados do problema e dos vetores unitários e . Utilize para o módulo da aceleração da gravidade.
(c) Considere agora os seguintes dados numéricos: , , , e . Calcule qual é a força média que o solo faz no sistema martelo-estaca durante o afundamento. Dê sua resposta utilizando o
Passo 1
Analisar o sistema
A primeira coisa que devemos fazer é entender como o sistema funciona. Dá uma olhada nesse exemplo de bate-estaca:
Meigo, não? O martelo seria o corpo no alto. Quando ele é liberado, melhor sair de baixo ou se não você será afundado ao invés da estaca!
Passo 2
Teorema Impulso-Momento Linear para o sistema martelo-estaca
Temos que tomar cuidado nessa pergunta porque ela pede o impulso do sistema martelo-estaca. Seria diferente a resposta se considerássemos somente o martelo, por exemplo. Agora que estamos de olho, vamos lembrar do Teorema Impulso-Momento Linear:
Num primeiro momento, nosso sistema martelo-estaca estava com velocidade , certo? Comparando esse instante com o instante em que o sistema para de afundar e fica no repouso, vamos ter:
Tá, mas e daí? Como essa expressão vai me ajudar? Bem, se lembrarmos da outra definição de impulso:
Opa, aí sim! Agora podemos calcular a força que o solo faz no sistema martelo-estaca até parar de afundar. Só substituir os valores e ser feliz:
Resposta
c)