Uma bola desloca-se com velocidade constante e colide elasticamente na lateral de uma mesa, segundo o ângulo definido entre a direção de seu movimento e a lateral da mesa e é claro que ; como mostra a figura. O processo de colisão dura um tempo . Na figura estão indicadas setas numeradas. A opção correta para representar a força média que atua na bola durante a colisão é:
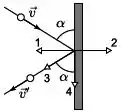
- ;
- ;
- ;
- ;
- nenhuma das respostas anteriores;
Passo 1
Como já vimos a força média está relacionada com o impulso como
Além disso, o impulso é
Para que eu escrevi isso tudo? Simples, repara que o vetor força média tem a mesma direção e sentido que a variação da velocidade, então para descobrir sua direção é só achar as velocidades e descobrir sua variação.
Passo 2
Começando pela velocidade inicial, você já viu algumas vezes como descobrir as componentes da velocidade, lembra? Usando a “regra do COlado/SEparado”.
Então cada componente fica
Na questão ele faz
Então a velocidade inicial fica
Passo 3
Agora vamos à velocidade final, temos que fazer a mesma coisa achando cada componente usando a “regra do COlado/SEparado”.
Na questão ele faz
Passo 4
Beleza, agora vamos achar a variação da velocidade
Passo 5
Repara que o sentido da variação da velocidade é para esquerda e só na horizontal, então a que representa a forma média é o vetor
Resposta
Letra D