[Enunciado comum às Questões 5 e 6]
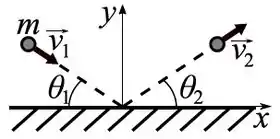
Uma bola de massa , movendo-se com velocidade colide com uma parede vertical, como mostra a figura abaixo. Depois da colisão, a bola tem velocidade . Os ângulos que os vetores e fazem com a parede são e , respectivamente. é o impulso exercido pela parede sobre o bloco durante a colisão.
[Questão 5]
Considere as afirmativas abaixo:
. Se as energias cinéticas antes e depois da colisão forem iguais, então .
. Se e , então possui apenas componente não nula.
. .
Marque a alternativa abaixo contendo apenas as assertivas corretas.
(a)
(b)
(c)
(d) e
(e) e
(f) e
(g) Todas
(h) Nenhuma
Passo 1
Quando a bola colide com a parede, a parede exerce uma força sobre a bola durante um certo intervalo de temp, ou seja, realiza um impulso sobre a bola que faz com que a direção da sua velocidade mude porém seu módulo se mantenha.
Vamos analisar as afirmativas.
Passo 2
. Se as energias cinéticas antes e depois da colisão forem iguais, então .
Isso está errado, pois a energia cinética não necessariamente está relacionada com haver impulso ou não.
Vai haver impulso quando uma certa força for aplicada no sistema por um intervalo de tempo, nesse caso, a bolinha.
Além disso, podemos garantir que houve um impulso diferente de zero nesse caso a partir do Teorema Impulso-Momento Linear:
Se o momento linear da bolinha é dado por:
Como o vetor velocidade mudou para (um vetor numa direção diferente), houve uma variação de momento linear não nula, logo houve um impulso não nulo também, por mais que a energia cinética tenha se mantido.
A afirmativa é falsa.
Passo 3
Vamos analisar a antes da .
. .
Para checar isso, vamos usar o Teorema Impulso-Momento Linear, pois é uma maneira de relacionar impulso com as velocidades final e inicial:
Então, vimos que a afirmativa é verdadeira.
Passo 4
. Se e , então possui apenas componente não nula.
Como queremos saber a direção do impulso , vamos partir da mesma relação que usamos no Pass 3 (anterior):
Agora, vamos decompor os vetores velocidade em suas componentes:
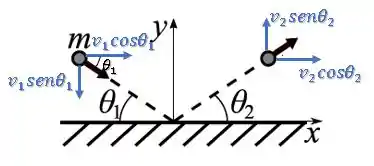
Como os módulos e são iguais, assim como os ângulos e , as componentes em se cancelam, sobrando apenas a componente em :
Substituindo isso no Teorema Impulso-Momento Linear:
Ou seja, o impulso realmente só vai ter uma componente em .
Isso faz sentido já que o impulso está na mesma direção que a força que a parede exerceu sobre a bolinha.
E se a componente em da velocidade da bolinha não se alterou, a força que a parede exerceu deve estar apenas na vertical (em ):
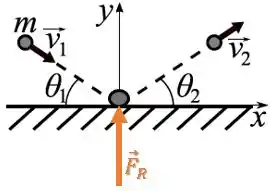
A afirmativa é verdadeira.
Apenas as afirmativas e estão corretas, ficamos com a letra (f).
Resposta
Letra (f)