Uma bola de massa e velocidade inicial se choca com uma esteira rolante, conforme a figura ao lado. A esteira está em movimento com velocidade para a direita. A bola incide sobre a esteira formando um ângulo , e após a colisão se afasta da superfície formando um ângulo , ambos em relação à normal. Considerando que a bola conserva sua energia cinética, identifique abaixo qual item correspondente ao componente do impulso ao longo da direção , .
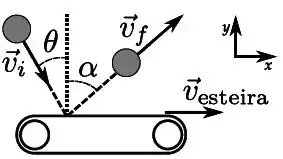
Dados: ; ; ; .
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Passo 1
Temos uma bola colidindo com uma esteira em movimento.
Caso a esteira estivesse parada, ela normalmente, só rebateria a bola na direção perpendicular à ela (força na direção do eixo ), porém, como ela está em movimento, ela exerce uma força na bola na direção do eixo .
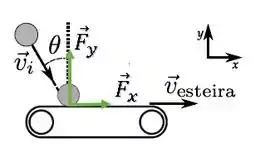
Ambas as forças vão gerar um impulso sobre a bola.
A questão pede o impulso na direção , ou seja queremos achar o impulso na direção do eixo .
Para isso, podemos pensar em calcular o impulso usando a expressão:
Entretanto, não sabemos o módulo da força média nessa colisão e muito menos o tempo de duração dessa situação.
Então, precisamos de um outro caminho...
Como nós temos informações, direta ou indiretamente, sobre as velocidades inicial e final, um bom jeito de encontrar o impulso sobre a bola nessa colisão é através do teorema impulso-momento linear:
Ou seja, se tivermos a variação do momento linear da bola, encontramos o impulso sobre ela.
Passo 2
Como a questão pede apenas o impulso na direção do eixo , podemos olhar para a variação de momento linear apenas em também:
Assim, temos:
Já temos o valor da massa , então basta nós encontrarmos quem são essas componentes em das velocidades inicial e final.
Passo 3
Na velocidade inicial, temos uma inclinação de com relação à normal:
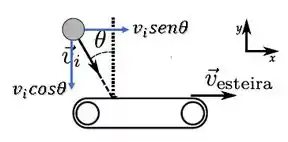
Logo, temos que sua componente em é:
Já a velocidade final, faz um ângulo desconhecido com a normal, porém conhecemos os valores de seu seno e cosseno, o que já e suficiente para a decomposição:
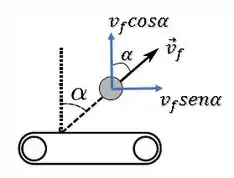
Logo, a componente em da velocidade final é:
Entretanto, ainda não temos o módulo de , mas relaxa que isso é bem tranquilo de encontrar.
Passo 4
O enunciado diz que a energia cinética da bolinha se conservou...
Qual a única maneira de um corpo conservar sua energia cinética (sem mudar a massa né hehe)?
Sim, apenas se o módulo de sua velocidade for o mesmo antes e depois da colisão:
Passo 5
Agora, vamos voltar ao cálculo do impulso :
Substituindo os valores temos:
Achamos o impulso que a esteira exerce sobre a bola na direção do eixo , ou seja, na direção .
Ficamos com a letra (g).
Resposta
Letra (g)