Exercícios de Teorema Impulso-Momento Linear - Lista de Exercícios Resolvida
Questão 1
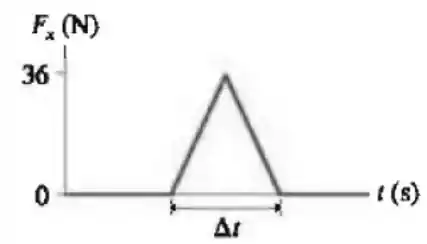
Considere dois processos distintos de colisão unidimensionais, A e B, entre duas partículas. A figura mostra a intensidade da força sobre uma das partículas em cada processo. A área sob as duas curvas é a mesma. Assinale a alternativa correta.
A intensidade do impulso exercido pela força nos dois eventos é a mesma.
A intensidade da força média é a mesma nos dois processos.
O momento linear de cada partícula não varia durante a colisão.
Nada se pode afirmar sobre a variação de momento linear nos dois processos, pois não conhecemos a velocidade das partículas envolvidas.
Nada se pode afirmar sobre a variação de momento linear nos dois processos, pois não sabemos se a colisão é inelástica ou não.
Ver solução completaQuestão 2
A figura mostra um carrinho de massa , sobre um trilho de ar, que comprime de uma mola de constante elástica . O carrinho está inicialmente preso ao suporte do trilho por um fio. O fio é cortado, e a mola expande-se empurrando o carrinho. Ao passar pela posição de equilíbrio da mola, , o carrinho perde contato com a mola. No trajeto até perder contato com a mola, o impulso fornecido ao carrinho foi igual a:
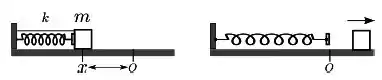
;
;
;
;
;
Ver solução completaQuestão 3
Uma bola de aço de massa igual a é largada de uma altura de sobre uma barra de aço horizontal. A bola é rebatida até uma altura de . a) Calcule o impulso comunicado para a bola durante a colisão. b) Sabendo que a bola permanece em contato com a barra durante , calcule a força média exercida sobre a bola durante a colisão.
Ver solução completaQuestão 4
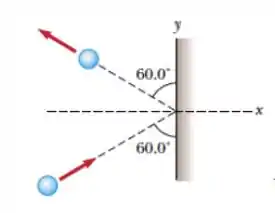
Uma bola de aço de bate em uma parede com a rapidez de a um ângulo com a superfície. Ela quica e recua com a mesma rapidez e mesmo ângulo, como apresentada na figura. Se a bola fica em contato com a parede por , qual é a intensidade da força média exercida pela parede sobre a bola?
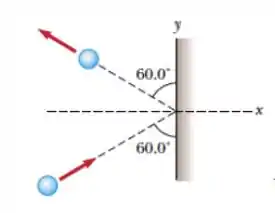
Questão 5
Um bate-estaca usa um motor de potência para levantar um martelo de massa até uma altura (relativa ao topo da estaca). Ao final do levantamento, a mesma é solta e bate sobre a haste sendo fixada no solo.
Qual o tempo de subida do martelo?
Qual a velocidade do martelo no momento de impacto?
Qual o impulso que o martelo transmite em um ciclo (entre o início da subida e o final do impacto)?
Se dobramos a potência do motor, e mantemos o mesmo tempo de subida, qual solução dará mais impulso ao martelo: dobrar a massa, ou dobrar a altura? Demonstre.
Dado .
Ver solução completaQuestão 6
Uma bola de beisebol de é golpeada por um bastão. Logo antes do impacto, a bola se desloca a horizontalmente da esquerda para direita e abandona o bastão quando ela se move com velocidade de para esquerda formando um ângulo de acima da horizontal. Se o bastão e a bola permaneceram em contato durante , calcule o módulo do componente horizontal e da componente vertical da força média do bastão sobre a bola.
Ver solução completaQuestão 7
Um bloco de massa repousa sobre um plano inclinado de um ângulo em relação à horizontal. O bloco é subitamente impulsionando, paralelamente ao plano, por uma marreta, parando após percorrer uma distância no plano inclinado, a partir de sua posição inicial, como mostra a figura. Sabendo-se que o coeficiente de atrito cinético entre o bloco e o plano é , determine:
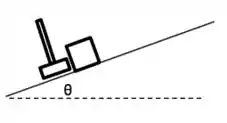
O trabalho realizado pela força de atrito durante o deslocamento ;
A velocidade do bloco, imediatamente após a marretada;
O valor do impulso que a marreta imprime o bloco.
Ver solução completaQuestão 8
A figura mostra um carrinho de massa , sobre um trilho de ar, que comprime de uma mola de constante elástica . O carrinho está inicialmente preso ao suporte do trilho por um fio. O fio é cortado, e a mola expande-se empurrando o carrinho. Ao passar pela posição de equilíbrio da mola, , o carrinho perde contato com a mola. No trajeto até perder contato com a mola, o impulso fornecido ao carrinho foi igual a:
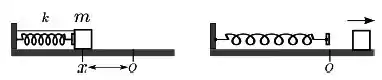
- ;
- ;
- ;
- ;
- ;
Questão 9
Uma partícula de massa é abandonada de uma altura em relação ao solo. Após se chocar com o solo, a partícula é ricocheteada de volta, e alcança a altura máxima , com . O módulo do impulso aplicado pelo solo na partícula foi de
(a)
(b)
(c)
(d)
Ver solução completaQuestão 10
Muitos automóveis têm os sacos do ar (air bags) instalados dentro dos painéis como uma medida de segurança. O impacto de uma colisão faz com que o saco de ar se infle, amortecendo a cabeça do motorista quando ela ou ele é jogado contra o painel do carro. Suponha que tal saco possa aumentar por um fator de 100 o tempo da colisão entre a cabeça do passageiro e o painel. Qual é o efeito que isto teria sobre a força média exercida na cabeça do motorista pelo painel?
a) A força seria reduzida por um fator de 10.
b) A força não mudaria.
c) A força seria reduzida por um fator de 1000.
d) A força seria reduzida por um fator de 50.
e) A força seria reduzida por um fator de 100.
Ver solução completaQuestão 12
Uma corrente de densidade linear constante, comprimento e massa está sobre uma mesa horizontal cujo comprimento é ligeiramente inferior a de modo que uma pequena parte da corrente, de comprimento desprezível, fica pendurada. A parte da corrente que está sobre a mesa começa aos poucos a deslizar sem atrito. Pede-se calcular:
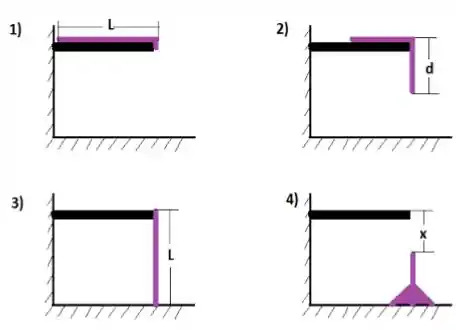
(a) o trabalho realizado pela força gravitacional quando o comprimento da parte pendurada atinge (item 2) da figura.
(b) a velocidade da corrente no instante em que a parte pendurada é igual a .
(c) a aceleração quando .
(d) Supondo agora que a corrente tenha escorregado completamente da mesa como mostra a figura acima (item 3), pede-se calcular a força exercida pelo solo sobre a corrente (força normal) após a corrente ter escorregado uma distancia igual a , como indicado pela figura acima (item 4). Suponha para tanto que a velocidade inicial com que a corrente começa a cair é nula.
Obs: Considere
Ver solução completaQuestão 13
Um bate-estaca usa um motor de potência para levantar um martelo de massa até uma altura (relativa ao topo da estaca). Ao final do levantamento, a mesma é solta e bate sobre a haste sendo fixada no solo.
Qual o tempo de subida do martelo?
Qual a velocidade do martelo no momento de impacto?
Qual o impulso que o martelo transmite em um ciclo (entre o início da subida e o final do impacto)?
Se dobramos a potência do motor, e mantemos o mesmo tempo de subida, qual solução dará mais impulso ao martelo: dobrar a massa, ou dobrar a altura? Demonstre.
Dado .
Ver solução completaQuestão 16
Uma bola de massa e velocidade inicial se choca com uma esteira rolante, conforme a figura ao lado. A esteira está em movimento com velocidade para a direita. A bola incide sobre a esteira formando um ângulo , e após a colisão se afasta da superfície formando um ângulo , ambos em relação à normal. Considerando que a bola conserva sua energia cinética, identifique abaixo qual item correspondente ao componente do impulso ao longo da direção , .
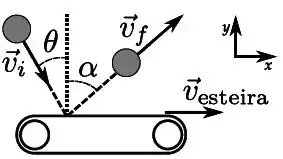
Dados: ; ; ; .
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 17
[ENUNCIADO COMUM ÀS QUESTÕES 6 e 7 do 2°EE 2017.2]
Uma bola de beisebol de massa colide com um taco a uma velocidade dada por . O impulso do taco sobre a bola é e o módulo da força média exercida pelo taco sobre a bola é de . Desconsidere o efeito da força peso da bola.
[Questão 7]
A velocidade da bola imediatamente após a colisão com o taco é
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 18
[ENUNCIADO COMUM ÀS QUESTÕES 6 e 7 do 2°EE 2017.2]
Uma bola de beisebol de massa colide com um taco a uma velocidade dada por . O impulso do taco sobre a bola é e o módulo da força média exercida pelo taco sobre a bola é de . Desconsidere o efeito da força peso da bola.
[Questão 6]
Julgue as seguintes assertivas.
(I) A velocidade da bola antes da colisão tem módulo .
(II) O momento linear da bola se conserva na colisão com o taco.
(III) A colisão tem duração de .
Estão corretas somente:
(a) I
(b) II
(c) III
(d) I e II
(e) I e III
(f) II e III
(g) Todas
(h) Nenhuma
Ver solução completaQuestão 21
Uma bola de aço de bate em uma parede com a rapidez de a um ângulo com a superfície. Ela quica e recua com a mesma rapidez e mesmo ângulo, como apresentada na figura. Se a bola fica em contato com a parede por , qual é a intensidade da força média exercida pela parede sobre a bola?
Questão 22
Um deslizador de trilho de ar com massa de 600 g colide com uma mola fixa em uma das extremidades do trilho. As figuras mostram a velocidade do deslizador e a força exercida sobre ele pela mola. Por quanto tempo o deslizador fica em contato com a mola?
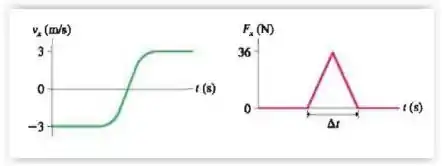
(A) 0,20s
(B) 0,40s
(C ) 0,10s
(D) 0,60s
(E) 0,30s
Ver solução completaQuestão 23
2) Um bloco de massa está ligado a uma mola de constante elástica e comprimento natural . O bloco é solto do repouso na posição e desliza para cima por uma haste lisa sob ação de uma força constante de módulo , que faz um ângulo com a vertical.
Adote para a aceleração da gravidade o valor .
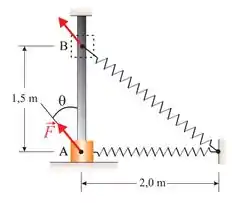
A velocidade do bloco na posição , em unidade do SI, é:
a)
b)
c)
d)
e)
Ver solução completaQuestão 24
Um tenista realiza um saque arremessando a bola verticalmente até uma altura máxima h em relação ao solo, na qual atinge a bola com a raquete. A bola sai com velocidade horizontal e suficiente para voar até atingir o solo a uma distância horizontal A da posição de saque. Sabendo que o tempo de colisão entre a raquete e a bola é ∆t e que a massa da bola é m, a força média exercida pela raquete sobre a bola durante o intervalo ∆t é:
Questão 25
A figura mostra um carrinho de massa m, sobre um trilho de ar, que comprime de x uma mola de constante elástica k. O carrinho está inicialmente preso ao suporte do trilho por um fio. O fio é cortado, e a mola expande-se empurrando o carrinho. Ao passar pela posição de equilíbrio da mola, O, o carrinho perde contato com a mola. No trajeto até perder contato com a mola, o impulso fornecido ao carrinho foi
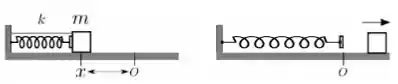
a)
b) 2
c)
d)
e)
Ver solução completaQuestão 26
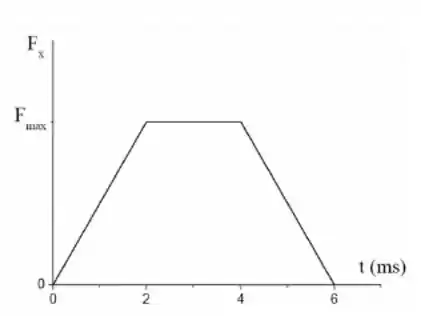
O gráfico abaixo mostra o comportamento com o tempo da força que um taco realiza sobre uma bola de golfe de massa , que está inicialmente em repouso quando atingida pelo taco. A força chega a um valor máximo em . Das afirmações que se seguem, assinale aquela que é INCORRETA.
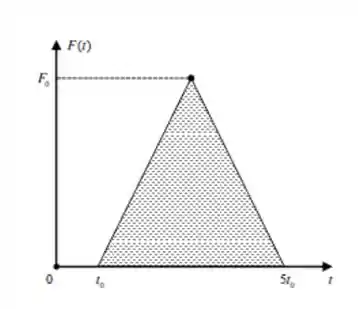
(a) O módulo do impulso produzido pelo taco é dado por
(b) A aceleração média da bola será
(c) A velocidade da bola após a tacada será
(d) A variação de momento linear da bola é fornecida pela área sombreada no gráfico
(e) A aceleração máxima da bola é
Ver solução completaQuestão 27
A figura representa a força sobre um corpo de massa igual a que está movendo-se ao longo do eixo. Se a velocidade do corpo é no instante , qual é a velocidade do corpo no instante ?
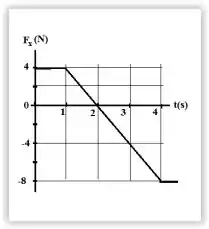
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 28
Um automóvel de está parado em um sinal de trânsito. Em um dado momento o mesmo passa a aumentar sua velocidade a uma taxa de . Sabendo que essa aceleração perdurou , determine o impulso aplicado ao automóvel.
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 31
[Enunciado comum às Questões 5 e 6]
Uma bola de massa , movendo-se com velocidade colide com uma parede vertical, como mostra a figura abaixo. Depois da colisão, a bola tem velocidade . Os ângulos que os vetores e fazem com a parede são e , respectivamente. é o impulso exercido pela parede sobre o bloco durante a colisão.
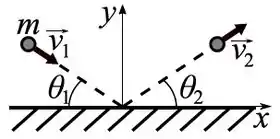
[Questão 6]
Suponha agora que a bola possui uma massa . Os ângulos satisfazem e , enquanto que . O tempo de colisão é igual a . Qual é a força média que a parede exerce sobre a bola?
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 32
Q - Uma bola de tênis de e com velocidade inicial colide com uma parede e retorna com velocidade de mesmo valor em módulo. A figura abaixo representa a força da parede sobre a bola durante a colisão. Sabendo-se que o tempo que dura a colisão entre a bola e a parede é , o máximo valor da força que a parede exerce sobre a bola durante a colisão, em Newtons, é:
• Considere a bola como uma partícula de massa .
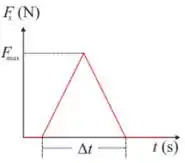
Questão 33
Q - Um carro de massa deslocando-se em uma trajetória retilínea com velocidade colide com um muro de concreto que resiste ao impacto (não se
deforma). Por causa da colisão, o carro deforma-se e o centro de massa desloca-se a distância
, na direção do muro, com desaceleração constante. Podemos afirmar que o módulo da força média, em Newtons, exercida pelo muro sobre o carro é:
Ver solução completaQuestão 34
Uma força de 5000 N é aplicada a um objeto, produzindo um impulso de módulo 1000 N.s.
Sabendo que a força é horizontal e para a direita, determine o tempo de contato da força sobre o corpo e a direção do impulso.
a) 0,4 s horizontal para a esquerda
b) 0,2 s horizontal para a esquerda
c) 0,2 s e horizontal para a direita
d) 0,6 s vertical para cima
e) 0,5 horizontal para a direita
Ver solução completaQuestão 35
O carro de um estudante estava com a bateria fraca. Ele pediu ajuda a dois amigos que, empurrando o carro durante , fizeram com que ele atingisse uma velocidade de . Se a massa do carro é de , qual foi a força média que os amigos aplicaram ao carro?
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 36
Uma bola de borracha de massa desliza sobre uma superfície horizontal sem atrito e colide com um anteparo fixo. O módulo da velocidade da bola é . A colisão faz um ângulo com a face do anteparo como ilustra a figura. A bola é refletida a mesma velocidade escalar e com o mesmo ângulo. O contato entre a bola e o anteparo dura . Utilize o sistema de coordenadas indicado.
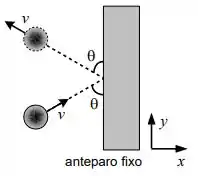
a) O que se pode afirmar sobre a conservação do momento linear da bola?
b) Calcule a força média do anteparo sobre a bola.
Ver solução completaQuestão 37
O carro de um estudante estava com a bateria fraca. Ele pediu ajuda a dois amigos que, empurrando o carro durante , fizeram com que ele atingisse uma velocidade de . Se a massa do carro é de , qual foi a força média que os amigos aplicaram ao carro?
Questão 38
Em uma colisão entre dois corpos de massas diferentes, como se comparam as magnitudes do impulso transmitido para o corpo de menor massa pelo corpo de maior massa e o impulso transmitido para o corpo maior massa pelo corpo de menor massa?
(A) O corpo de menor massa recebe um impulso maior.
(B) O corpo de maior massa recebe um impulso maior.
(C) Ambos os corpos recebem o mesmo impulso.
(D) A resposta depende da razão entre as massas.
(E) A resposta depende da razão entre as rapidezes.
Ver solução completaQuestão 39
Um objeto de , inicialmente em repouso, é submetido à força variável dada na figura ao lado. Qual é a variação do momento linear do objeto entre e ?
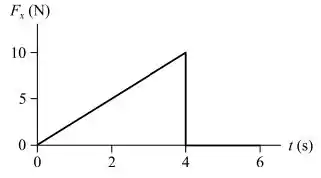
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 40
Ao desferir a primeira machadada, a personagem da tirinha movimenta vigorosamente seu machado, que atinge a árvore com energia cinética de .

Como a lâmina de aço tem massa , desconsiderando-se a inércia do cabo, o impulso transferido para a árvore na primeira machadada, em foi de:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 41
Uma manga cai de uma altura de sobre uma calçada. Quando uma segunda manga, idêntica à primeira, cai da mesma altura sobre a areia fofa, no mesmo nível da calçada, a duração da colisão é vezes maior. Em ambos os casos, a colisão é perfeitamente inelástica. Em comparação com a colisão na calçada, o impulso, a variação do momento e a força média experimentados pela segunda manga durante a colisão com a areia são, respectivamente:
(a) igual, maior, menor;
(b) igual, menor, maior;
(c) menor, igual, maior;
(d) igual, igual, menor;
(e) menor, menor, menor;
(f) igual, igual, igual;
Ver solução completaQuestão 42
Em um treinamento voltado para a preparação física de jogadores de futebol, um treinador constatou que sempre que era conferido uma força de na bola, o goleiro conseguia pegá-la. Estimando-se a massa da bola em e o tempo do chute de , determine o módulo da velocidade da bola imediatamente após o chute.
(a) .
(b) .
(c) .
(d) .
(e) .
Ver solução completaQuestão 43
Um jogador dá um chute em uma bola aplicando-lhe uma força de intensidade em em direção ao gol e o goleiro manifesta reação de defesa ao chute, mas a bola entra para o delírio da torcida. Determine a intensidade do impulso do chute que o jogador dá na bola para fazer o gol.
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 44
Jason desliza em linha reta ao longo de uma superfície plana com seus esquis movidos a jato. A massa combinada de Jason e esquis é de (a massa do combustível é desprezível) e Jason parte do repouso. Devido ao funcionamento do motor é exercida uma força de sobre os esquis para impulsioná los. O coeficiente de atrito cinético entre os esquis e a água é de . Infelizmente, os esquis ficam sem combustível depois de apenas . O quão longe Jason viaja até finalmente parar?
A)
B)
C)
D)
E)
Ver solução completaQuestão 45
Suponha que uma bola de ping-pong e uma bola de boliche rolam em direção a você, ambas com o mesmo momento linear. De forma a parar as duas bolas, você faz uma força de igual intensidade nas duas. Como os intervalos de tempo necessários para parar as duas bolas se comparam:
a) o intervalo de tempo para parar a bola de ping-pong é menor.
b) ambos intervalos de tempo são iguais.
c) o intervalo de tempo para parar a bola de ping-pong é maior.
Ver solução completaQuestão 46
Um bloco de massa repousa sobre um plano inclinado de um ângulo em relação à horizontal. O bloco é subitamente impulsionando, paralelamente ao plano, por uma marreta, parando após percorrer uma distância no plano inclinado, a partir de sua posição inicial, como mostra a figura. Sabendo-se que o coeficiente de atrito cinético entre o bloco e o plano é , determine:
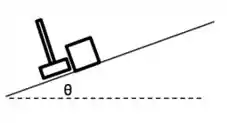
O trabalho realizado pela força de atrito durante o deslocamento ;
A velocidade do bloco, imediatamente após a marretada;
O valor do impulso que a marreta imprime o bloco.
Ver solução completaQuestão 47
Em um jogo de golf, o jogador aplica uma força de contato do taco com a bola. Com a tecnologia atual, é possível medir a força média aplicada por ele e o tempo de contato entre o taco e a bola. Considerando que a força média aplicada multiplicada pelo tempo de contato é o impulso da bola, pode-se afirmar que esse produto é igual a:
(a) Variação da Energia cinética da bola devido a rebatida.
(b) Variação da Quantidade de movimento linear da bola devido a rebatida.
(c) Energia potencial da bola devido a rebatida
(d) Quantidade de movimento angular da bola devido a rebatida.
(e) Quantidade de movimento linear da bola devido a rebatida.
Ver solução completaQuestão 48
A figura abaixo mostra o gráfico aproximado do módulo da força em função do tempo para a colisão de uma bola de massa contra uma parede. O valor do módulo da força máxima é desconhecido. A velocidade da bola imediatamente antes da colisão é , perpendicular à parede. A bola ricocheteia praticamente com o mesmo módulo da velocidade também perpendicular à parede.
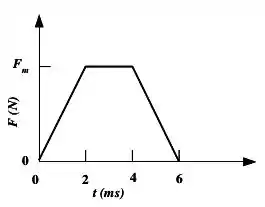
a) Calcule o impulso fornecido pela parede sobre a bola
b) Calcule o módulo da força máxima
Ver solução completaQuestão 49
Uma bolinha de borracha de massa cai a partir do repouso de uma altura , bate no chão e retorna à mesma altura de onde havia sido solta (um choque elástico com o chão), conforme mostra a figura.
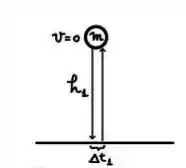
Seja a duração do choque entre a bolinha e o chão para este primeiro experimento. O gráfico da força exercida pelo chão sobre a bolinha é mostrado na figura abaixo, podendo ser aproximado por uma constante durante o intervalo e fora do intervalo.
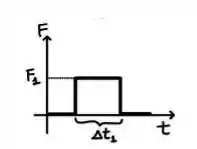
Caso o experimento seja repetido com (novamente um choque elástico) e o gráfico de seja similar, com uma força constante durante um intervalo , podemos afirmar que:
(a) Se , então
(b) independentemente de e
(c) Se , então
(d)
(e) Se , então
(f) então
(g)
Ver solução completaQuestão 50
Um pedaço de pedra de está deslizando a da esquerda para a direita sobre uma superfície horizontal sem atrito, quando é repentinamente atingida por um objeto que exerce uma grande força horizontal sobre ela, por um curto intervalo de tempo. O gráfico na figura abaixo mostra o módulo desta força em função do tempo.
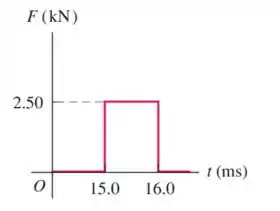
(a) Qual é o impulso que essa força exerce sobre a pedra?
Ver solução completaQuestão 51
Um gato com massa se move ao longo de uma linha reta (eixo x). A figura abaixo mostra um gráfico da velocidade do gato como função do tempo. Qual é a intensidade máxima da força resultante sobre o gato?
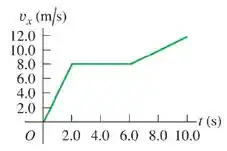
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 52
Um jogador de vôlei salta, a partir do repouso, para executar uma ação de bloqueio. Se a variação máxima da altura do seu centro de massa foi de no salto e o tempo de contato com o solo antes do salto foi de , podemos afirmar que o módulo da força média exercida pelo chão sobre ele (utilize )
é igual a do seu peso.
é igual a do seu peso.
é igual ao dobro do seu peso.
é igual ao seu peso.
é igual a do seu peso.
Ver solução completaQuestão 53
O fundo de uma caixa cheia d’água está situado a 10 m de altura acima de um piso horizontal e possui um furo por onde desce, a partir do repouso, um filete de água com uma taxa fixa de massa por tempo dada por . Quando atinge o piso o filete exerce uma força média vertical de impacto () sobre o piso, ficando com velocidade vertical nula . Calcule o valor dessa força média de impacto a partir do teorema do Impulso-Variação do Momento Linear.

Questão 54
Na colisão entre dois objetos de massas diferentes, como se relacionam os módulos dos impulsos aplicados sobre cada objeto?
Ambos os objetos recebem o mesmo impulso.
O objeto mais pesado recebe um impulso maior.
O objeto mais leve recebe um impulso maior.
A resposta depende da razão entre as massas.
A resposta depende da razão entre as velocidades.
Ver solução completaQuestão 55
Uma bola desloca-se com velocidade constante e colide elasticamente na lateral de uma mesa, segundo o ângulo definido entre a direção de seu movimento e a lateral da mesa e é claro que ; como mostra a figura. O processo de colisão dura um tempo . Na figura estão indicadas setas numeradas. A opção correta para representar a força média que atua na bola durante a colisão é:
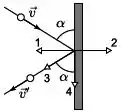
- ;
- ;
- ;
- ;
- nenhuma das respostas anteriores;
Questão 56
Um bate-estaca de gravidade funciona com um princípio muito simples. Um martelo de massa é solto do repouso a uma altura acima de uma estaca de massa . A colisão dura um intervalo de tempo muito curto . Imediatamente após a colisão o martelo e a estaca adquirem a mesma velocidade e chegam ao repouso, depois de afundarem uma distância . Suponha o intervalo de tempo de afundamento como sendo . Todo movimento acontece ao longo da direção vertical. Utilize o sistema de coordenadas abaixo, dê suas respostas em função dos dados do problema e dos vetores unitários e . Utilize para o módulo da aceleração da gravidade.
(c) Considere agora os seguintes dados numéricos: , , , e . Calcule qual é a força média que o solo faz no sistema martelo-estaca durante o afundamento. Dê sua resposta utilizando o
Ver solução completaQuestão 57
Um bate-estaca de gravidade funciona com um princípio muito simples. Um martelo de massa é solto do repouso a uma altura acima de uma estaca de massa . A colisão dura um intervalo de tempo muito curto . Imediatamente após a colisão o martelo e a estaca adquirem a mesma velocidade e chegam ao repouso, depois de afundarem uma distância . Suponha o intervalo de tempo de afundamento como sendo . Todo movimento acontece ao longo da direção vertical. Utilize o sistema de coordenadas abaixo, dê suas respostas em função dos dados do problema e dos vetores unitários e . Utilize para o módulo da aceleração da gravidade.
(b) Determine o impulso resultante na estaca durante a colisão.
Ver solução completaQuestão 58
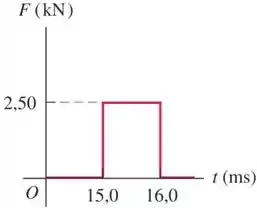
11 - Uma pedra de está deslizando a da esquerda para a direita sobre uma superfície horizontal sem atrito, quando é repentinamente atingida por um objeto que exerce uma grande força horizontal sobre ela, por um curto período. O gráfico na figura mostra o módulo dessa força em função do tempo. Qual é o impulso que essa força exerce sobre a pedra?
A)
B)
C)
D)
E)
Questão 60
E novamente ele chegou com inspiração
Com muito amor, com emoção, com explosão em gol
Sacudindo a torcida aos 33 minutos do segundo tempo
Depois de fazer uma jogada celestial em gol
Tabelou, driblou dois zagueiros
Deu um toque driblou o goleiro
Só não entrou com bola e tudo
Porque teve humildade em gol
Trecho da música Filho Maravilha de Jorge BenJor.
Originalmente, o nome dessa música era Fio Maravilha, em homenagem ao jogador do Flamengo, porém, ao recusar a homenagem, o compositor trocou o nome da música para Filho Maravilha. Fio Maravilha recebeu o apelido da torcida após marcar o gol da vitória (1 a 0) de uma partida da equipe carioca contra o Benfica, de Portugal. Esse é o gol descrito na música de Benjor. Somos capazes de visualizá-lo através dos versos. Imagine Fio tabelando, driblando dois zagueiros e depois o goleiro. Neste momento ele chuta a bola para o gol com uma força de durante . O Impulso causado por essa força na bola foi de:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 61
Em Ímola, o melhor piloto do mundo acelerou, bateu e morreu.
As imagens ficarão gravadas como um raio na memória dos brasileiros.
Na sétima volta do Grande Prêmio de San Marino, no autódromo de ímola, na Itália, Ayrton Senna passa direto pela curva Tamburello, a quilômetros por hora, e espatifa-se no muro de concreto. à 1h40 da tarde, hora do Brasil, um boletim médico do hospital Maggiore de Bolonha, para onde o piloto foi levado de helicóptero, anunciou a morte cerebral de Ayrton Senna. Não havia mais nada a fazer. Ayrton Senna da Silva, 34 anos, tricampeão mundial de Fórmula 1, 41 vitórias em Grandes Prêmios, 65 pole-positions, um dos maiores fenômenos de todos os tempos no automobilismo, estava morto.
Fonte: veja.abril.com.br/especiais/extras/fechado/senna01.html. acesso: 02/11/2011 as 9:11.
De acordo com os dados da reportagem e sabendo que a massa de Ayrton Senna era de e que a massa de um fórmula 1 é, aproximadamente, . O Impulso gerado pela força da batida no muro foi de, aproximadamente:
Obs: e
(a) , sentido da velocidade do carro.
(b) , sentido da velocidade do carro.
(c) , sentido contrário da velocidade do carro.
(d) 2, sentido contrário da velocidade do carro.
(e) , sentido contrário da velocidade do carro.
Ver solução completaQuestão 62
Dê as respostas em notação científica, no sistema internacional de unidades considerando rigorosamente o conceito de algarismos significativos.
Considere um bloco que possui momento linear que sofre uma colisão e tem seu momento linear alterado para . Durante a colisão o bloco sofre uma aceleração média de módulo . Determine a massa do bloco sabendo que a colisão durou um intervalo de tempo .
Ver solução completaQuestão 63
3. Uma bola de borracha e outra de argila de mesma massa são arremessadas contra uma parede com velocidades inicias iguais. A bola de borracha ricocheteia e a de argla gruda na parede. Qual delas exerce maior impulso sobre a parede?
- A bola de argila, pois ela fica grudada.
- A bola de borracha, pois ela ricocheteia.
- Elas exercem impulsos iguais, pois possuem massas e velocidades iniciais iguais.
- Não há impulso, pois a parede não se move.
- A bola de argila, pois a parede exercesse um impulso maior sobre esta bola.
Questão 64
Atletas olímpicos da modalidade 100 metros rasos devem produzir uma força de impulsão () durante um curto intervalo de tempo no momento da largada. Tipicamente a duração deste impulso é 0,10s e a velocidade imediatamente após o impulso é 4,0 m/s. Considerando que a força de impulsão é constante ao longo da sua duração e assumindo, o módulo de é equivalente a:
a) força peso do atleta
b) 2 vezes a força peso do atleta
c) 4 vezes a força peso do atleta
d) 20 vezes a força peso do atleta
e) 40 vezes a força peso do atleta
Ver solução completaQuestão 65
3. Uma bola de borracha e outra de argila de mesma massa são arremessadas contra uma parede com velocidades inicias iguais. A bola de borracha ricocheteia e a de argla gruda na parede. Qual delas exerce maior impulso sobre a parede?
- A bola de argila, pois ela fica grudada.
- A bola de borracha, pois ela ricocheteia.
- Elas exercem impulsos iguais, pois possuem massas e velocidades iniciais iguais.
- Não há impulso, pois a parede não se move.
- A bola de argila, pois a parede exercesse um impulso maior sobre esta bola.
Questão 66
Considere dois processos distintos de colisão unidimensionais, A e B, entre duas partículas. A figura mostra a intensidade da força sobre uma das partículas em cada processo. A área sob as duas curvas é a mesma. Assinale a alternativa correta.
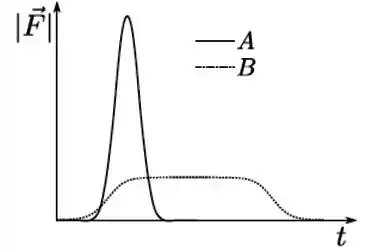
(a) A intensidade do impulso exercido pela força nos dois eventos é a mesma.
(b) A intensidade da força média é a mesma nos dois processos.
(c) O momento linear de cada partícula não varia durante a colisão.
(d) Nada se pode afirmar sobre a variação de momento linear nos dois processos, pois não conhecemos a velocidade das partículas envolvidas.
(e) Nada se pode afirmar sobre a variação de momento linear nos dois processos, pois não sabemos se a colisão é inelástica ou não.
Ver solução completaQuestão 67
Considere uma bola de tênis e uma bola de boliche que serão arremessadas na sua direção para que você as agarre. Se as bolas tem a mesma energia cinética quando chegam a você, para fazê-las parar completamente é correto afirmar que:
(a) O módulo do impulso e o trabalho que você deve realizar serão os mesmos sobre a bola de tênis e sobre a de boliche.
(b) Tanto o módulo do impulso quanto o trabalho que você deve realizar serão menores sobre a bola de tênis do que sobre a bola de boliche.
(c) O trabalho que você deve realizar será o mesmo para ambas as bolas mas o módulo do impulso sobre a bola de boliche será maior do que sobre a de tênis.
(d) O módulo do impulso necessário será a mesmo para ambas as bolas mas o trabalho realizado sobre a bola de boliche precisará ser maior.
(e) O módulo do impulso necessário será maior sobre a bola de tênis mas o trabalho realizado deverá ser maior sobre a bola de boliche.
Ver solução completaQuestão 68
1) Uma bola de borracha é abandonada da altura de e rebate no solo atingindo acima do piso. A bola fica em contato com o piso por cerca de . Determine a aceleração média da bola durante o contato com o piso em módulo, direção e sentido.
Ver solução completaQuestão 69
Uma bola de tênis de massa está se aproximando, em linha reta, e a , de um jogador. O jogador a rebate de volta com velocidade de . Se a bola permaneceu em contacto com a raquete, qual foi o módulo da força média exercida sobre a bola?
a)
b)
c)
d)
e)
Ver solução completaQuestão 70
13) Uma bola de massa m cai de uma altura h ricocheteia e sobe até dois terços da altura inicial. Qual é o módulo do impulso exercido pelo piso sobre a bola? Considere o módulo da aceleração da gravidade e despreze a resistência do ar.
(a)
(b) (c)
(d)
(e)
Ver solução completaQuestão 71
Um avião explode no ar e se divide em três partes, cujas massas e velocidades imediatamente depois da explosão são (unidades no SI):
.
a. Qual era a velocidade do avião ao explodir?
Ver solução completaQuestão 72
Um avião explode no ar e se divide em três partes, cujas massas e velocidades imediatamente depois da explosão são (unidades no SI):
.
b. Qual era o seu momento linear?
Ver solução completaQuestão 73
Um atirador, com um rifle de apoiado ao ombro, dispara uma bala de , cuja velocidade na boca da arma é de .
Que impulso transmite ao ombro do atirador?
Ver solução completaQuestão 74
Uma bala de 10 g é disparada sobre um pêndulo balístico de massa 990 g.
a. Se a velocidade inicial da bala é 300 m/s, qual a altura atingida pelo pêndulo (junto com a bala) depois da colisão?
Ver solução completaQuestão 75
Um atirador, com um rifle de apoiado ao ombro, dispara uma bala de , cuja velocidade na boca da arma é de .
Com que velocidade inicial a arma recua?
Ver solução completaQuestão 76
Um atirador, com um rifle de apoiado ao ombro, dispara uma bala de , cuja velocidade na boca da arma é de .
Se o impulso é absorvido pelo ombro em , qual é a força média exercida sobre ele?
Ver solução completaQuestão 77
Uma bala de 10 g é disparada sobre um pêndulo balístico de massa 990 g.
b. Se a velocidade inicial da bala é 200 m/s, determine a altura máxima atingida pelo pêndulo quando a bala passa através dele e emerge com velocidade de 50 m/s.
Ver solução completaQuestão 78
Um bloco de madeira, de 1, 0 kg, está ligado a uma mola de constante de força 200 N/m e repousa sobre uma superfície horizontal lisa. Uma bala de 20 g atinge o bloco e comprime a mola de 13, 3 cm.
a. Calcular a velocidade da bala antes da colisão.
Ver solução completaQuestão 79
Um bloco de madeira, de 1, 0 kg, está ligado a uma mola de constante de força 200 N/m e repousa sobre uma superfície horizontal lisa. Uma bala de 20 g atinge o bloco e comprime a mola de 13, 3 cm.
b. Que fração da energia mecânica inicial se perde na colisão?
Ver solução completaQuestão 80
Um corpo é arremessado diversas vezes em um plano horizontal sem atrito contra uma parede vertical, com a mesma energia cinética inicial, porém de uma posição diferente, a cada vez.
A figura mostra uma vista superior das trajetórias descritas pelo corpo em cada lançamento, designadas por , e .
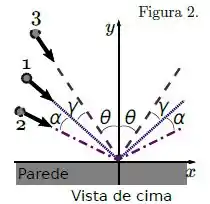
Sejam , e os impulsos produzidos pela parede sobre o corpo referentes às trajetórias , e respectivamente. Assinale a alternativa correta:
Questão 81
Uma força de é aplicada a um objeto, produzindo um impulso de módulo Sabendo que a força é horizontal e para a direita, determine o tempo de contato da força sobre o corpo e a direção do impulso.
a) e horizontal para a direita
b) horizontal para a esquerda
c) horizontal para a esquerda
d) vertical para cima
e) horizontal para a direita
Ver solução completaQuestão 82
Em uma tacada de baseball, a força de interação entre o taco e a bola varia com o tempo de acordo com o gráfico ao lado. Desta curva, determine (a) o impulso fornecido à bola, (b) a força média exercida sobre a bola, e (c) a força máxima exercida sobre a bola.
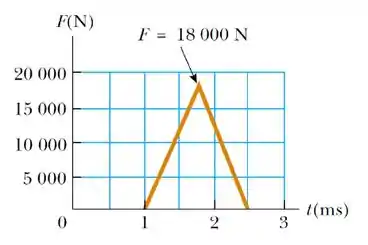
Questão 83
Duas pequenas esferas de massas e , , colidem frontalmente na ausência de forças externas. Após a colisão elas movimentam-se juntas. Durante a colisão, atuam em cada esfera as forças médias e nas esferas de massa M e m respectivamente. Qual é a relação entre as forças médias que atuaram
nas esferas durante a colisão?
a)
b)
c)
d)
e) Sem o conhecer o tempo que durou a colisão, não é possível obter uma relação entre as forças.
Ver solução completaQuestão 85
Uma esfera de massa é lançada em um trilho unidimensional de atrito desprezível com velocidade ao encontro de uma segunda esfera lançada simultaneamente de massa desconhecida com velocidade . As esferas colidem elasticamente e durante a colisão a primeira esfera sofre uma força dada pelo gráfico abaixo.
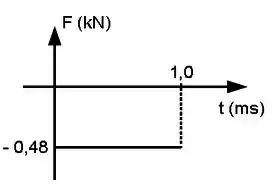
(d) Determine e os impulsos nas duas esferas
Ver solução completaQuestão 86
Dois blocos de massas e deslizam sem atrito sobre uma superfície horizontal. O bloco M desliza para leste com rapidez de e colide com o bloco m que desliza para oeste com rapidez de . Após a colisão os blocos ficam colados. O gráfico abaixo mostra a variação com o tempo do módulo da força exercida por um bloco sobre o outro durante a colisão. Qual é o valor de no gráfico?
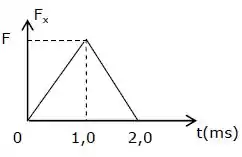
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 87
[Enunciado comum às Questões 5 e 6]
Uma bola de massa , movendo-se com velocidade colide com uma parede vertical, como mostra a figura abaixo. Depois da colisão, a bola tem velocidade . Os ângulos que os vetores e fazem com a parede são e , respectivamente. é o impulso exercido pela parede sobre o bloco durante a colisão.
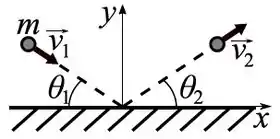
[Questão 5]
Considere as afirmativas abaixo:
. Se as energias cinéticas antes e depois da colisão forem iguais, então .
. Se e , então possui apenas componente não nula.
. .
Marque a alternativa abaixo contendo apenas as assertivas corretas.
(a)
(b)
(c)
(d) e
(e) e
(f) e
(g) Todas
(h) Nenhuma
Ver solução completaQuestão 88
Uma pequena esfera se desloca sobre uma mesa horizontal lisa quando colide com uma parede, conforme figura a seguir.
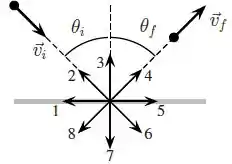
Sabe-se que os módulos das velocidades da esfera antes e depois da colisão são iguais e que esses vetores velocidade fazem o mesmo ângulo com a direção normal à parede . Qual dos vetores numerados na figura que melhor representa a força que a parede exerce sobre a esfera?
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 89
Uma bola de borracha de massa e outra de argila de mesma massa são arremessadas contra uma parede com velocidades iniciais iguais. Qual delas exerce o maior impulso sobre a parede?
(a) A bola de argila, pois ela fica grudada
(b) A bola de borracha, pois ela ricocheteia
(c) Elas exercem impulsos iguais, pois possuem mesmas massas e velocidades iniciais
(d) Não há impulso, pois a parede não se move
(e) A bola de argila, pois a parede exerce um impulso maior sobre esta bola
Ver solução completa