Uma bolinha de borracha de massa cai a partir do repouso de uma altura , bate no chão e retorna à mesma altura de onde havia sido solta (um choque elástico com o chão), conforme mostra a figura.
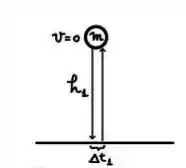
Seja a duração do choque entre a bolinha e o chão para este primeiro experimento. O gráfico da força exercida pelo chão sobre a bolinha é mostrado na figura abaixo, podendo ser aproximado por uma constante durante o intervalo e fora do intervalo.
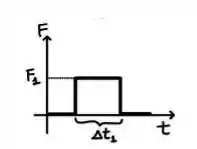
Caso o experimento seja repetido com (novamente um choque elástico) e o gráfico de seja similar, com uma força constante durante um intervalo , podemos afirmar que:
(a) Se , então
(b) independentemente de e
(c) Se , então
(d)
(e) Se , então
(f) então
(g)
Passo 1
Como a bolinha retorna à mesma altura da qual ela foi solta, concluímos que o choque da bolinha com o chão é elástico. No entanto, nas duas situações podemos calcular a velocidade com que a bolinha chega no chão e consequentemente a velocidade com que ela sai do chão usando conservação de energia mecânica:
Como , temos:
Passo 2
Usando o teorema do impulso também conseguimos concluir que:
E isto vale nos dois casos, portanto:
Como :
Resposta
(d)