Uma bola de borracha de massa desliza sobre uma superfície horizontal sem atrito e colide com um anteparo fixo. O módulo da velocidade da bola é . A colisão faz um ângulo com a face do anteparo como ilustra a figura. A bola é refletida a mesma velocidade escalar e com o mesmo ângulo. O contato entre a bola e o anteparo dura . Utilize o sistema de coordenadas indicado.
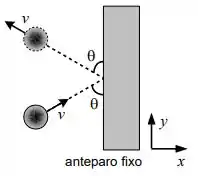
a) O que se pode afirmar sobre a conservação do momento linear da bola?
b) Calcule a força média do anteparo sobre a bola.
Passo 1
Na letra (a), queremos saber se o momento linear da bola se conserva.
E aí, se conserva?
O momento linear da bola é dado por:
Lembrando que é um vetor com direção e sentido.
Pensa comigo, se a velocidade da bola mudou de direção, o momento linear também mudou.
Entãooooo... ele não se conserva!
Mas por que não se conserva?
Ah isso é porque o nosso sistema é apenas a bolinha, ou seja quando ela bate no anteparo, ela exerce uma força sobre ela, uma força externa. Assim, o sistema (bolinha) não está livre da ação de forças externas.
Não confunda com a situação de uma colisão entre duas partículas soltas (sistema isolado).
Passo 2
Na letra (b), queremos a força média sobre a bolinha durante a colisão.
Já vimos que essa força externa vai atuar na bolinha. Assim, ela vai gerar um impulso sobre a bolinha.
Podemos relacionar isso com a variação de momento linear dela a partir do teorema impulso-momento linear:
Aqui, poderíamos abrir esses vetores e escrever separadamente uma equação para e outra para . Mas vamos deixar direto na forma vetorial, que você vai ver que uma das componentes se mantêm igual.
Momento linear é dado por:
Então:
Passo 3
Vamos decompor as velocidades inicial e final.
Inicial:
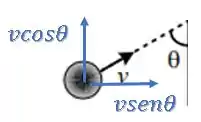
Repare que a componente horizontal que será com “” e a vertical que será com “”, pois o ângulo não é o ângulo de inclinação do vetor com a horizontal (padrão) e sim a inclinação do vetor com a vertical.
Final:
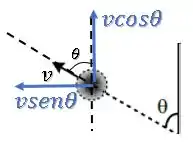
Passo 4
Voltando à nossa expressão, temos:
Substituindo os valores, temos:
Então, achamos o vetor força média:
Passo 5
Passo 5
Resposta
(a) O momento linear da bolinha não se conserva pois há uma força externa atuando sobre ela durante a colisão.
(b)