Considere dois processos distintos de colisão unidimensionais, A e B, entre duas partículas. A figura mostra a intensidade da força sobre uma das partículas em cada processo. A área sob as duas curvas é a mesma. Assinale a alternativa correta.

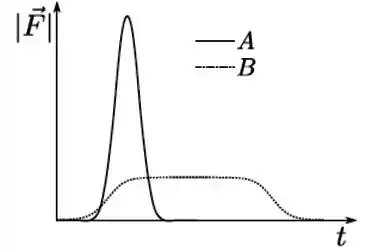
(a) A intensidade do impulso exercido pela força nos dois eventos é a mesma.

(b) A intensidade da força média é a mesma nos dois processos.

(c) O momento linear de cada partícula não varia durante a colisão.

(d) Nada se pode afirmar sobre a variação de momento linear nos dois processos, pois não conhecemos a velocidade das partículas envolvidas.

(e) Nada se pode afirmar sobre a variação de momento linear nos dois processos, pois não sabemos se a colisão é inelástica ou não.

Alternativa (b):

A intensidade da força média é dada pelo teorema força impulso:

Já vimos que pros 2 processos, o impulso é o mesmo, então pra força média ser a mesma, os das 2 colisões também têm que ser iguais.

Esse é o tempo em que age a força, e pelo gráfico fica claro que o processo B dura bem mais tempo que o A:

Então a alternativa é falsa.

Alternativa (c):

Vamos lá, mais uma fórmula com o impulso, dessa vez a da variação do momento linear:

Ou, em módulo:

Já vimos que o impulso é a área sob o gráfico. E essa área claramente não é nula, nas duas curvas. Ou seja:

Então há sim variação do momento linear da partícula nos 2 processos, a alternativa é falsa.

Alternativa (d) e (e):

Acabamos de ver que podemos afirmar que a variação de momento linear da partícula nos processos não é nula. Inclusive podemos ver que ela é positiva, pois a área sob as curvas é positiva.

Então essas duas alternativas estão erradas.